232 Courses
-
Differential Equations
-

The Geometrical View of y'=f(x,y): Direction Fields, Integral Curves
-

Euler's Numerical Method for y'=f(x,y) and its Generalizations
-

Solving First-order Linear ODE's; Steady-state and Transient Solutions
-

First-order Substitution Methods: Bernouilli and Homogeneous ODE's
-

First-order Autonomous ODE's: Qualitative Methods, Applications
-

Complex Numbers and Complex Exponentials
-

First-Order Linear with Constant Coefficients
-

Applications to Temperature, Mixing, RC-circuit, Decay, and Growth Models
-
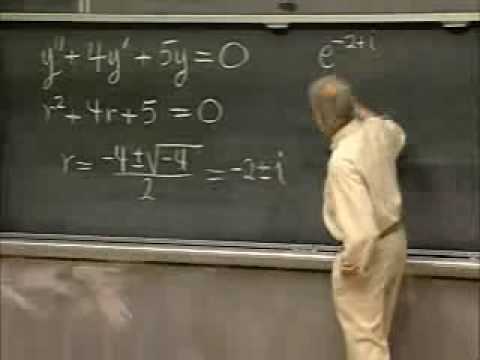
Solving Second-Order Linear ODE's with Constant Coefficients
-

Complex Characteristic Roots; Undamped and Damped Oscillations
-
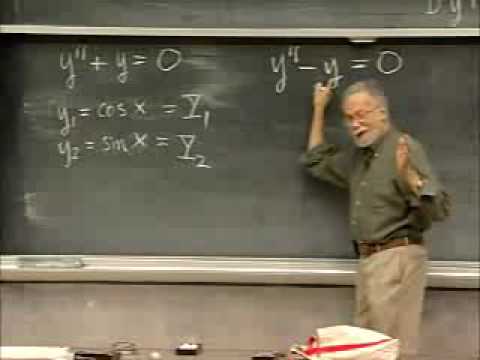
Second-Order Linear Homogeneous ODE's: Superposition, Uniqueness, Wronskians
-

Inhomogeneous ODE's; Stability Criteria for Constant-Coefficient ODE's
-

Inhomogeneous ODE's: Operator and Solution Formulas Involving Ixponentials
-

Interpretation of the Exceptional Case: Resonance
-
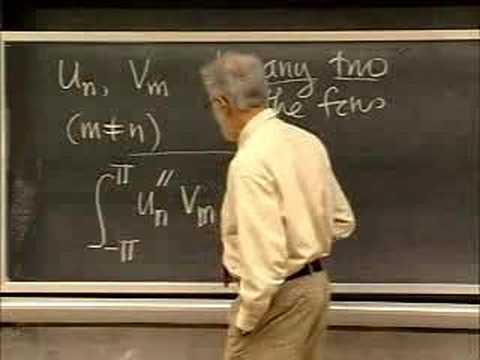
Introduction to Fourier Series; Basic Formulas for Period 2(pi)
-

More General Periods; Even and Odd Functions; Periodic Extension
-

Finding Particular Solutions via Fourier Series; Resonant Terms
-

Derivative Formulas; Using the Laplace Transform to Solve Linear ODE's
-

Convolution Formula: Proof, Connection with Laplace Transform, Application
-

Using Laplace Transform to Solve ODE's with Discontinuous Inputs
-

Impulse Inputs; Dirac Delta Function, Weight and Transfer Functions
-

First-Order Systems of ODE's; Solution by Elimination, Geometric Interpretation
-

Homogeneous Linear Systems with Constant Coefficients: Solution via Matrix Eigenvalues
-
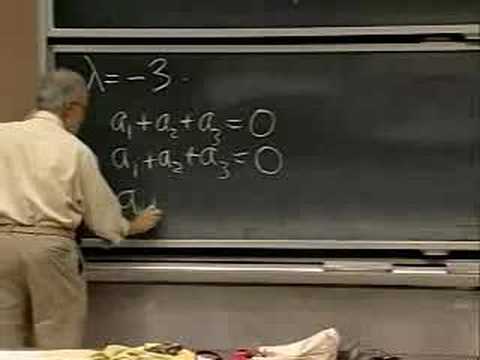
Continuation: Repeated Real Eigenvalues, Complex Eigenvalues
-

Sketching Solutions of 2x2 Homogeneous Linear System with Constant Coefficients
-

Matrix Methods for Inhomogeneous Systems
-

Matrix Exponentials; Application to Solving Systems
-

Decoupling Linear Systems with Constant Coefficients
-

Non-linear Autonomous Systems: Finding the Critical Points and Sketching Trajectories
-

Limit Cycles: Existence and Non-existence Criteria
-
Non-Linear Systems and First-Order ODE's
-
-
Digital Typography
-
Directed Evolution: Engineering Biocatalysts
-
Discrete Stochastic Processes
-

Introduction and Probability Review
-

More Review: The Bernoulli Process
-

Law of Large Numbers, Convergence
-

Poisson (the Perfect Arrival Process)
-

Poisson Combining and Splitting
-

From Poisson to Markov
-

Finite-state Markov Chains: The Matrix Approach
-

Markov Eigenvalues and Eigenvectors
-

Markov Rewards and Dynamic Programming
-

Renewals and the Strong Law of Large Numbers
-
Renewals: Strong Law and Rewards
-

Renewal Rewards, Stopping Trials, and Wald's Inequality
-

Little, M/G/1, Ensemble Averages
-

The Last Renewal
-

Renewals and Countable-State Markov
-

Countable-State Markov Chains
-

Countable-State Markov Chains and Processes
-

Countable-State Markov Processes
-

Markov Processes and Random Walks
-

Hypothesis Testing and Random Walks
-

Random Walks and Thresholds
-

Martingales (Plain, Sub, and Super)
-

Martingales: Stopping and Converging
-

Putting It All Together
-
-
Drugs, Politics, and Culture
-
Dynamic Optimization & Economic Applications (Recursive Methods)
-
Dynamic Optimization Methods with Applications
-
Dynamic Systems and Control
-
Dynamics of Nonlinear Systems