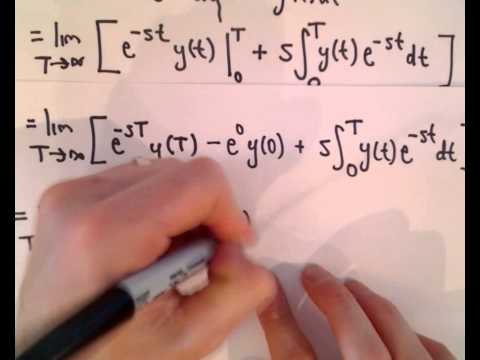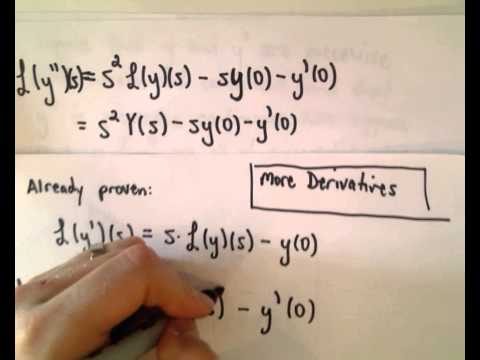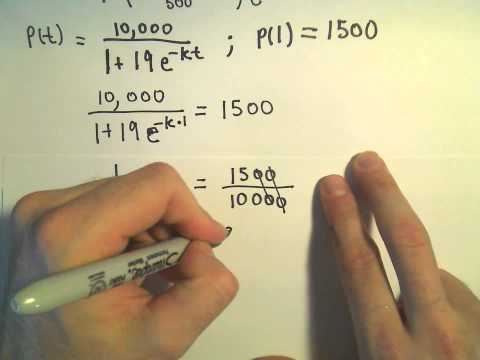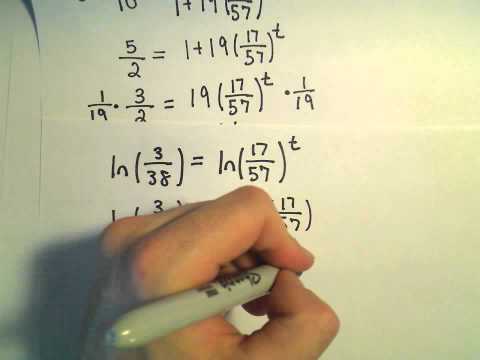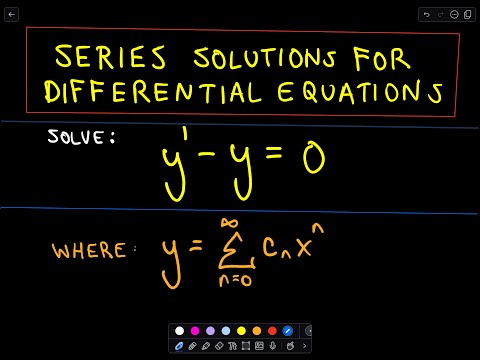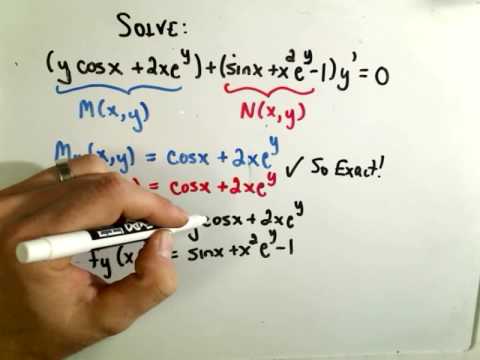Free Online Lectures and Courses for Mathematics

40 Courses

• Differential & Integral Calculus, Math 31A

  View Course
  • 

    Differential & Integral Calculus, Math 31A, Part 1

    Steve Butler 00:37:26
  • 

    Differential & Integral Calculus, Math 31A, Part 2

    Steve Butler 00:45:37
  • 

    Differential & Integral Calculus, Math 31A, Part 3

    Steve Butler 00:46:41
  • 

    Differential & Integral Calculus, Math 31A, Part 4

    Steve Butler 00:51:20
  • 

    Differential & Integral Calculus, Math 31A, Part 5

    Steve Butler 00:42:04
  • 

    Differential & Integral Calculus, Math 31A, Part 6

    Steve Butler 00:39:32
  • 

    Differential & Integral Calculus, Math 31A, Part 7

    Steve Butler 00:43:35
  • 

    Differential & Integral Calculus, Math 31A, Part 8

    Steve Butler 00:49:41
  • 

    Differential & Integral Calculus, Math 31A, Part 9

    Steve Butler 00:47:54
  • 

    Differential & Integral Calculus, Math 31A, Part 10

    Steve Butler 00:49:38
  • 

    Differential & Integral Calculus, Math 31A, Part 11

    Steve Butler 00:49:27
  • 

    Differential & Integral Calculus, Math 31A, Part 12

    Steve Butler 00:48:30
  • 

    Differential & Integral Calculus, Math 31A, Part 13

    Steve Butler 00:48:08
  • 

    Differential & Integral Calculus, Math 31A, Part 14

    Steve Butler 00:48:34
  • 

    Differential & Integral Calculus, Math 31A, Part 15

    Steve Butler 00:44:21
  • 

    Differential & Integral Calculus, Math 31A, Part 16

    Steve Butler 00:46:44
  • 

    Differential & Integral Calculus, Math 31A, Part 17

    Steve Butler 00:40:36
  • 

    Differential & Integral Calculus, Math 31A, Part 18

    Steve Butler 00:45:10
  • 

    Differential & Integral Calculus, Math 31A, Part 19

    Steve Butler 00:48:08
  • 

    Differential & Integral Calculus, Math 31A, Part 20

    Steve Butler 00:31:08
  • 

    Differential & Integral Calculus, Math 31A, Part 21

    Steve Butler 00:50:32
  • 

    Differential & Integral Calculus, Math 31A, Part 22

    Steve Butler 00:50:32
  • 

    Differential & Integral Calculus, Math 31A, Part 23

    Steve Butler 00:51:15
  • 

    Differential & Integral Calculus, Math 31A, Part 24

    Steve Butler 00:49:24
  • 

    Differential & Integral Calculus, Math 31A, Part 25

    Steve Butler 00:41:49

• Differential Equations

  View Course
  • 

    The Geometrical View of y'=f(x,y): Direction Fields, Integral Curves

    Arthur Mattuck 00:48:55
  • 

    Euler's Numerical Method for y'=f(x,y) and its Generalizations

    Arthur Mattuck 00:50:43
  • 

    Solving First-order Linear ODE's; Steady-state and Transient Solutions

    Arthur Mattuck 00:50:22
  • 

    First-order Substitution Methods: Bernouilli and Homogeneous ODE's

    Arthur Mattuck 00:50:11
  • 

    First-order Autonomous ODE's: Qualitative Methods, Applications

    Arthur Mattuck 00:45:44
  • 

    Complex Numbers and Complex Exponentials

    Arthur Mattuck 00:45:26
  • 

    First-Order Linear with Constant Coefficients

    Arthur Mattuck 00:41:10
  • 

    Applications to Temperature, Mixing, RC-circuit, Decay, and Growth Models

    Arthur Mattuck 00:50:35
  • 

    Solving Second-Order Linear ODE's with Constant Coefficients

    Arthur Mattuck 00:49:58
  • 

    Complex Characteristic Roots; Undamped and Damped Oscillations

    Arthur Mattuck 00:46:23
  • 

    Second-Order Linear Homogeneous ODE's: Superposition, Uniqueness, Wronskians

    Arthur Mattuck 00:50:31
  • 

    Inhomogeneous ODE's; Stability Criteria for Constant-Coefficient ODE's

    Arthur Mattuck 00:46:24
  • 

    Inhomogeneous ODE's: Operator and Solution Formulas Involving Ixponentials

    Arthur Mattuck 00:47:54
  • 

    Interpretation of the Exceptional Case: Resonance

    Arthur Mattuck 00:44:25
  • 

    Introduction to Fourier Series; Basic Formulas for Period 2(pi)

    Arthur Mattuck 00:49:31
  • 

    More General Periods; Even and Odd Functions; Periodic Extension

    Arthur Mattuck 00:49:28
  • 

    Finding Particular Solutions via Fourier Series; Resonant Terms

    Arthur Mattuck 00:45:44
  • 

    Derivative Formulas; Using the Laplace Transform to Solve Linear ODE's

    Arthur Mattuck 00:51:05
  • 

    Convolution Formula: Proof, Connection with Laplace Transform, Application

    Arthur Mattuck 00:44:19
  • 

    Using Laplace Transform to Solve ODE's with Discontinuous Inputs

    Arthur Mattuck 00:44:08
  • 

    Impulse Inputs; Dirac Delta Function, Weight and Transfer Functions

    Arthur Mattuck 00:44:54
  • 

    First-Order Systems of ODE's; Solution by Elimination, Geometric Interpretation

    Arthur Mattuck 00:47:02
  • 

    Homogeneous Linear Systems with Constant Coefficients: Solution via Matrix Eigenvalues

    Arthur Mattuck 00:49:05
  • 

    Continuation: Repeated Real Eigenvalues, Complex Eigenvalues

    Arthur Mattuck 00:46:36
  • 

    Sketching Solutions of 2x2 Homogeneous Linear System with Constant Coefficients

    Arthur Mattuck 00:50:25
  • 

    Matrix Methods for Inhomogeneous Systems

    Arthur Mattuck 00:46:52
  • 

    Matrix Exponentials; Application to Solving Systems

    Arthur Mattuck 00:48:51
  • 

    Decoupling Linear Systems with Constant Coefficients

    Arthur Mattuck 00:47:05
  • 

    Non-linear Autonomous Systems: Finding the Critical Points and Sketching Trajectories

    Arthur Mattuck 00:47:09
  • 

    Limit Cycles: Existence and Non-existence Criteria

    Arthur Mattuck 00:45:52
  • 

    Non-Linear Systems and First-Order ODE's

    Arthur Mattuck 00:50:09

• Differential Equations

  View Course
  • 

    Introduction to Differential Equations

    Salman Khan 00:11:02
  • 

    Separable Differential Equations

    Salman Khan 00:12:00
  • 

    Separable Differential Equations II

    Salman Khan 00:05:37
  • 

    Exact Equations Intuition Part 1 (proofy)

    Salman Khan 00:09:54
  • 

    Exact Equations Intuition Part 2 (proofy)

    Salman Khan 00:10:51
  • 

    Exact Equations Example 1

    Salman Khan 00:12:09
  • 

    Exact Equations Example 2

    Salman Khan 00:08:01
  • 

    Exact Equations Example 3

    Salman Khan 00:09:59
  • 

    Integrating Factors 1

    Salman Khan 00:10:16
  • 

    Integrating Factors 2

    Salman Khan 00:08:26
  • 

    First Order Homogeneous (Part 1)

    Salman Khan 00:07:21
  • 

    First Order Homogeneous (Part 2)

    Salman Khan 00:08:22
  • 

    2nd Order Linear Homogeneous Differential Equations 1

    Salman Khan 00:09:44
  • 

    2nd Order Linear Homogeneous Differential Equations 2

    Salman Khan 00:08:28
  • 

    2nd Order Linear Homogeneous Differential Equations 3

    Salman Khan 00:05:59
  • 

    2nd Order Linear Homogeneous Differential Equations 4

    Salman Khan 00:09:10
  • 

    Complex Roots of the Characteristic Equations 1

    Salman Khan 00:10:27
  • 

    Complex Roots of the Characteristic Equations 2

    Salman Khan 00:10:23
  • 

    Complex Roots of the Characteristic Equations 3

    Salman Khan 00:10:12
  • 

    Repeated Roots of the Characteristic Part 1

    Salman Khan 00:11:58
  • 

    Repeated Roots of the Characteristic Part 2

    Salman Khan 00:08:52
  • 

    Undetermined Coefficients 1

    Salman Khan 00:10:11
  • 

    Undetermined Coefficients 2

    Salman Khan 00:11:00
  • 

    Undetermined Coefficients 3

    Salman Khan 00:08:09
  • 

    Undetermined Coefficients 4

    Salman Khan 00:05:54
  • 

    Laplace Transfrom 1

    Salman Khan 00:08:01
  • 

    Laplace Transfrom 2

    Salman Khan 00:07:34
  • 

    Laplace Transfrom 3

    Salman Khan 00:10:44
  • 

    Laplace Transfrom 4

    Salman Khan 00:09:13
  • 

    Laplace Transfrom 5

    Salman Khan 00:11:36
  • 

    Laplace Transform 6

    Salman Khan 00:09:45
  • 

    Laplace Transform to Solve an Equation

    Salman Khan 00:10:51
  • 

    Laplace Transform Solves an Equation 2

    Salman Khan 00:10:46
  • 

    More Laplace Transform Tools

    Salman Khan 00:11:17
  • 

    Using the Laplace Transform to Solve a Nonhomogeneous Equation

    Salman Khan 00:18:48
  • 

    Laplace Transform of: L(t)

    Salman Khan 00:09:06
  • 

    Laplace Transform of t^n: L(t^n)

    Salman Khan 00:10:16
  • 

    Laplace Transform of the the Unit Step

    Salman Khan 00:24:15
  • 

    Inverse Laplace Examples

    Salman Khan 00:19:15
  • 

    Laplace/Step Function Differential

    Salman Khan 00:19:12
  • 

    Dirac Delta Function

    Salman Khan 00:17:48
  • 

    Laplace Transform of the Dirac Delta

    Salman Khan 00:12:13
  • 

    Introduction to the Convolution

    Salman Khan 00:18:59
  • 

    The Convolution and the Laplace

    Salman Khan 00:13:46
  • 

    Using the Convolution Theorem to Solve an Intial Value Prob

    Salman Khan 00:12:14

• Differential Equations

  View Course
  • 

    Logistic Differential Equation

    Patrick Jones 00:05:20
  • 

    Euler's Method - Another Example #1

    Patrick Jones 00:05:35
  • 

    Euler's Method - Another Example #2

    Patrick Jones 00:05:53
  • 

    Solving a Separable Differential Equation, Another Example #1

    Patrick Jones 00:03:40
  • 

    Solving a Separable Differential Equation, Another Example #2

    Patrick Jones 00:02:04
  • 

    Solving a Separable Differential Equation, Another Example #3

    Patrick Jones 00:01:21
  • 

    Solving a Separable Differential Equation, Another Example #4, Initial Condition

    Patrick Jones 00:04:24
  • 

    Solving a Separable Differential Equation, Another Example #5, Initial Condition

    Patrick Jones 00:04:20
  • 

    Basic Differential Equation with an Initial Condition

    Patrick Jones 00:02:00
  • 

    Differential Equations - Basic Idea of What It Means to be a Solution

    Patrick Jones 00:03:47
  • 

    First Order Linear Differential Equations / Integrating Factors - Ex 2

    Patrick Jones 00:03:30
  • 

    Change of Variables / Homogeneous Differential Equation - Example 1

    Patrick Jones 00:07:39
  • 

    Change of Variables / Homogeneous Differential Equation - Example 2

    Patrick Jones 00:08:31
  • 

    Change of Variables / Homogeneous Differential Equation - Example 3

    Patrick Jones 00:05:52
  • 

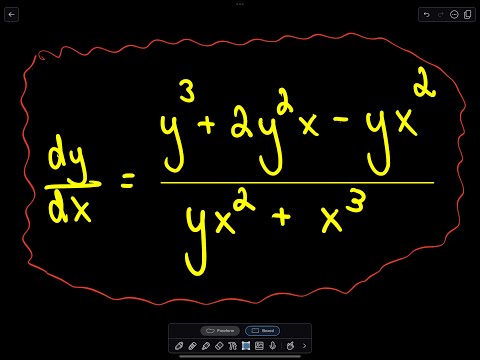
    Change of Variables / Homogeneous Differential Equation - Example 4

    Patrick Jones 00:12:12
  • 

    The Inverse Laplace Transform - Example and Important Theorem

    Patrick Jones 00:05:36
  • 

    Table of Laplace Transforms

    Patrick Jones 00:01:13
  • 

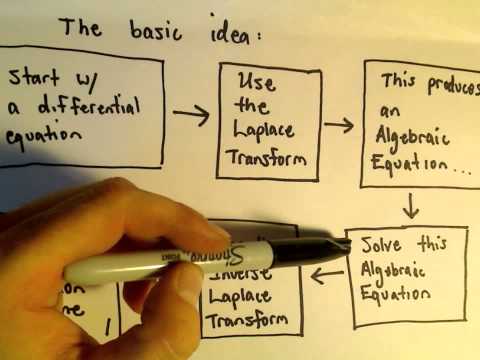
    The Laplace Transform - The Basic Idea of How We Use It

    Patrick Jones 00:01:33
  • 

    Laplace Transform is a Linear Operator - Proof

    Patrick Jones 00:03:36
  • 

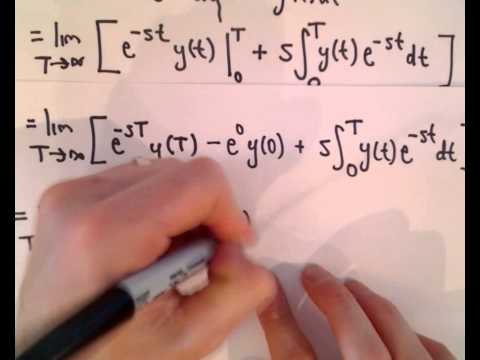
    The Laplace Transform, Basic Properties - Definitions and Derivatives

    Patrick Jones 00:13:09
  • 

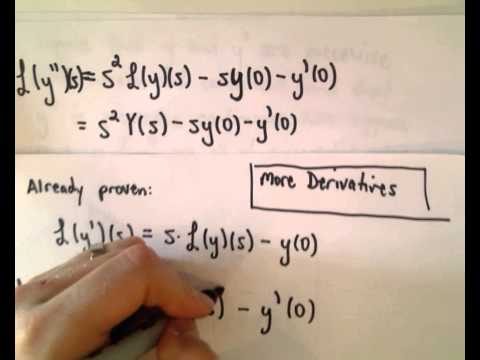
    The Laplace Transform - More Derivatives

    Patrick Jones 00:04:13
  • 

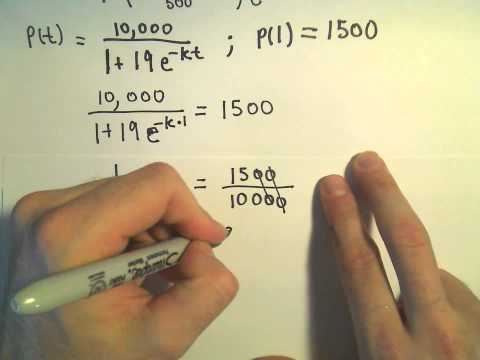
    The Logistic Equation and Models for Population - Example 1, part 1

    Patrick Jones 00:07:04
  • 

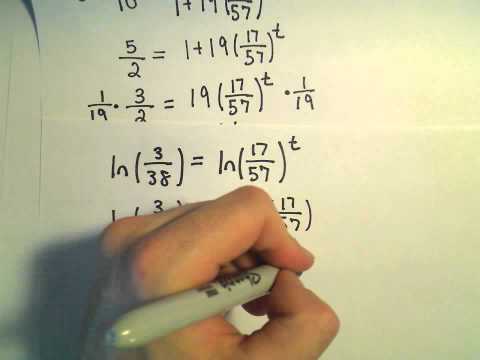
    The Logistic Equation and Models for Population - Example 1, part 2

    Patrick Jones 00:05:09
  • 

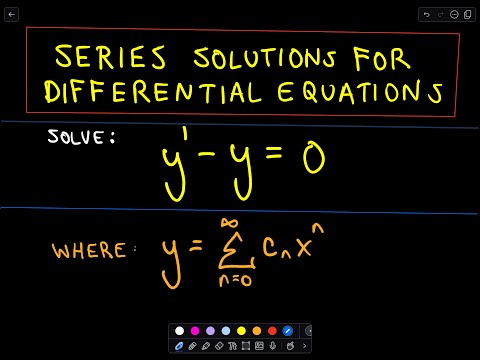
    Power Series Solutions of Differential Equations

    Patrick Jones 00:11:45
  • 

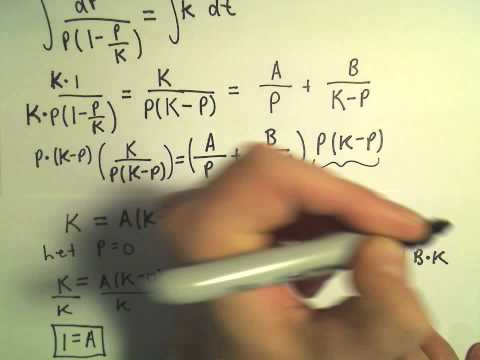
    The Logistic Equation and the Analytic Solution

    Patrick Jones 00:12:10
  • 

    Exact Differential Equations

    Patrick Jones 00:05:48
  • 

    First Order Linear Differential Equations

    Patrick Jones 00:05:48

• Discrete Stochastic Processes

  View Course
  • 

    Introduction and Probability Review

    Robert Gallager 01:16:27
  • 

    More Review: The Bernoulli Process

    Robert Gallager 01:08:20
  • 

    Law of Large Numbers, Convergence

    Robert Gallager 01:21:28
  • 

    Poisson (the Perfect Arrival Process)

    Robert Gallager 01:17:14
  • 

    Poisson Combining and Splitting

    Robert Gallager 01:24:32
  • 

    From Poisson to Markov

    Robert Gallager 01:19:17
  • 

    Finite-state Markov Chains: The Matrix Approach

    Robert Gallager 00:55:34
  • 

    Markov Eigenvalues and Eigenvectors

    Robert Gallager 01:23:38
  • 

    Markov Rewards and Dynamic Programming

    Robert Gallager 01:23:36
  • 

    Renewals and the Strong Law of Large Numbers

    Robert Gallager 01:21:53
  • 

    Renewals: Strong Law and Rewards

    Robert Gallager 01:18:17
  • 

    Renewal Rewards, Stopping Trials, and Wald's Inequality

    Robert Gallager 01:26:22
  • 

    Little, M/G/1, Ensemble Averages

    Robert Gallager 01:14:53
  • 

    The Last Renewal

    Robert Gallager 01:15:44
  • 

    Renewals and Countable-State Markov

    Robert Gallager 01:19:40
  • 

    Countable-State Markov Chains

    Robert Gallager 01:23:46
  • 

    Countable-State Markov Chains and Processes

    Robert Gallager 01:16:29
  • 

    Countable-State Markov Processes

    Robert Gallager 01:22:15
  • 

    Markov Processes and Random Walks

    Robert Gallager 01:23:09
  • 

    Hypothesis Testing and Random Walks

    Robert Gallager 01:25:23
  • 

    Random Walks and Thresholds

    Robert Gallager 01:21:17
  • 

    Martingales (Plain, Sub, and Super)

    Robert Gallager 01:22:40
  • 

    Martingales: Stopping and Converging

    Robert Gallager 01:20:44
  • 

    Putting It All Together

    Robert Gallager 01:21:27

• Early Mathematics

  View Course
  • 

    Early Mathematics: A Short Introduction

    Robin Wilson 00:41:48
  • 

    Mathematics in Neolithic Scotland

    Tony Mann 00:21:17
  • 

    Exploring Ancient Greek and Roman Numeracy

    Serafina Cuomo 00:43:33
  • 

    Decoding the Heavens: Solving the mystery of the World's First Computer

    Jo Marchant 00:34:59
  • 

    Vedic Mathematics: My Trip to India to Uncover the Truth

    Alex Bellos 00:34:00

• Engineering Mathematics

  View Course
  • 

    Partial Derivatives + PDEs Tutorial

    Chris Tisdell 00:09:16
  • 

    Chain Rule + Partial Derivatives

    Chris Tisdell 00:08:54
  • 

    Taylor Polynomials + Functions of Two Variables

    Chris Tisdell 00:10:37
  • 

    Partial Derivatives + Error Estimation

    Chris Tisdell 00:12:14
  • 

    Differentiate Under Integral Signs: Leibniz Rule

    Chris Tisdell 00:10:48
  • 

    How to Find + Classify Critical Points of Functions

    Chris Tisdell 00:11:51
  • 

    Finding Critical Points of Functions

    Chris Tisdell 00:14:34
  • 

    Method of Lagrange Multipliers

    Chris Tisdell 00:18:43
  • 

    Lagrange Multipliers: An Example

    Chris Tisdell 00:11:09
  • 

    Lagrange Multipliers: 2 Constraints

    Chris Tisdell 00:11:01
  • 

    Vector Functions of One Variable Tutorial

    Chris Tisdell 00:13:28
  • 

    Gradient of A Function

    Chris Tisdell 00:14:59
  • 

    Divergence of Vector Fields

    Chris Tisdell 00:13:37
  • 

    Curl of Vector Fields

    Chris Tisdell 00:13:57
  • 

    Line Integrals

    Chris Tisdell 00:16:07
  • 

    Div, Curl + Line Integral Examples

    Chris Tisdell 00:18:14
  • 

    Flux In The Plane. Line Integrals

    Chris Tisdell 00:17:03
  • 

    Curl, Grad and Line Integral Examples

    Chris Tisdell 00:14:06
  • 

    Simple Double Integral

    Chris Tisdell 00:11:04
  • 

    Tutorial - Double Integrals

    Chris Tisdell 00:07:39
  • 

    Reverse The Order In Double Integrals

    Chris Tisdell 00:11:48
  • 

    Double Integrals + Area

    Chris Tisdell 00:10:06
  • 

    Polar Coordinates and Double Integrals

    Chris Tisdell 00:10:25
  • 

    Double Integrals & Polar Co-Ordinates

    Chris Tisdell 00:16:14
  • 

    Centroid and Double Integrals

    Chris Tisdell 00:13:34
  • 

    Center of Mass + Double Integrals

    Chris Tisdell 00:11:40
  • 

    Linear, First-Order Differential Equations

    Chris Tisdell 00:11:35
  • 

    Homogeneous First Order Ordinary Differential Equation

    Chris Tisdell 00:07:32
  • 

    How to Solve 2nd Order Differential Equations

    Chris Tisdell 00:15:53
  • 

    Nonhomogeneous 2nd-Order Differential Equations

    Chris Tisdell 00:26:58
  • 

    Variation of Constants / Parameters

    Chris Tisdell 00:13:52
  • 

    Principal Axes Theorem Tutorial

    Chris Tisdell 00:15:05
  • 

    Intro to Laplace Transform + How to Calculate Them

    Chris Tisdell 00:08:42
  • 

    First Shifting Theorem of Laplace Transforms

    Chris Tisdell 00:12:00
  • 

    Second Shifting Theorem: Laplace Transforms

    Chris Tisdell 00:10:31
  • 

    Laplace Transforms + Differential Equations

    Chris Tisdell 00:12:40
  • 

    Intro to Fourier Series & How to Calculate Them

    Chris Tisdell 00:13:46
  • 

    Fourier Series: Odd & Even Functions

    Chris Tisdell 00:46:59
  • 

    Fourier Series Review

    Chris Tisdell 00:28:25
  • 

    Fourier Series & Differential Equations

    Chris Tisdell 00:17:41
  • 

    Heat Equation Derivation

    Chris Tisdell 00:15:45
  • 

    Heat Equation: Separation of Variables

    Chris Tisdell 00:47:14
  • 

    Heat Equation + Fourier Series

    Chris Tisdell 00:20:53
  • 

    Wave Equation + Fourier Series + Separation of Variables

    Chris Tisdell 00:47:08
  • 

    Separable Differential Equations

    Salman Khan 00:12:00

• Geometry

  View Course
  • 

    Introduction to Angles

    Salman Khan 00:09:55
  • 

    Angles Part 2

    Salman Khan 00:09:04
  • 

    Angles Part 3

    Salman Khan 00:09:47
  • 

    Angles Formed Between Transversals and Parallel Lines

    Salman Khan 00:07:53
  • 

    Angles of Parallel Lines 2

    Salman Khan 00:05:15
  • 

    The Angle Game

    Salman Khan 00:09:01
  • 

    Similar Triangles

    Salman Khan 00:09:34
  • 

    Similar Triangles 2

    Salman Khan 00:09:54
  • 

    Area and Perimeter

    Salman Khan 00:12:20
  • 

    Circles: Radius, Diameter, and Circumference

    Salman Khan 00:11:05
  • 

    The Pythagorean Theorem

    Salman Khan 00:10:46
  • 

    The Pythagorean Theorem II

    Salman Khan 00:09:36
  • 

    45-45-90 Triangles

    Salman Khan 00:09:30
  • 

    Intro to 30-60-90 Triangles

    Salman Khan 00:09:39
  • 

    30-60-90 Triangles II

    Salman Khan 00:04:49
  • 

    Heron's Formula

    Salman Khan 00:04:43
  • 

    Part 1 of Proof of Heron's Formula

    Salman Khan 00:10:59
  • 

    Part 2 of Proof of Heron's Formula

    Salman Khan 00:12:08
  • 

    An Inscribed Angle is Half of a Central Angle that Subtends the Same Arc

    Salman Khan 00:14:16
  • 

    Area of Inscribed Equilateral Triangle (Some Basic Trig Used) 2

    Salman Khan 00:11:39
  • 

    Right Triangles Inscribed in Circles

    Salman Khan 00:05:35
  • 

    Area of Inscribed Equilateral Triangle (Some Basic Trig Used)

    Salman Khan 00:04:36

• Highlights of Calculus

  View Course
  • 

    Professor Strang Introduces the Series

    Gilbert Strang 00:04:57
  • 

    Big Picture of Calculus

    Gilbert Strang 00:37:47
  • 

    Big Picture: Derivatives

    Gilbert Strang 00:30:05
  • 

    Max and Min and Second Derivatives

    Gilbert Strang 00:38:31
  • 

    The Exponential Function

    Gilbert Strang 00:38:54
  • 

    Big Picture: Integrals

    Gilbert Strang 00:37:22

• Introduction to Linear Dynamical Systems

  View Course
  • 

    Overview of Linear Dynamical Systems

    Stephen Boyd 01:16:46
  • 

    Linear Functions (Continued)

    Stephen Boyd 01:05:52
  • 

    Linearization (Continued)

    Stephen Boyd 01:19:11
  • 

    Nullspace of a Matrix (Continued)

    Stephen Boyd 01:14:08
  • 

    Orthonormal Set of Vectors

    Stephen Boyd 01:15:14
  • 

    Least-Squares

    Stephen Boyd 01:16:19
  • 

    Least-Squares Polynomial Fitting

    Stephen Boyd 01:15:46
  • 

    Multi-Objective Least-Squares

    Stephen Boyd 01:15:58
  • 

    Least-Norm Solution

    Stephen Boyd 01:09:02
  • 

    Examples of Autonomous Linear Dynamical Systems

    01:11:42
  • 

    Solution via Laplace Transform and Matrix Exponential

    Stephen Boyd 01:08:55
  • 

    Time Transfer Property

    Stephen Boyd 01:13:37
  • 

    Markov Chain (Example)

    Stephen Boyd 01:13:01
  • 

    Jordan Canonical Form

    Stephen Boyd 01:17:42
  • 

    DC or Static Gain Matrix

    Stephen Boyd 01:09:01
  • 

    RC Circuit (Example)

    Stephen Boyd 01:12:35
  • 

    Gain of a Matrix in a Direction

    Stephen Boyd 01:16:52
  • 

    Sensitivity of Linear Equations to Data Error

    Stephen Boyd 01:15:14
  • 

    Reachability

    Stephen Boyd 01:10:30
  • 

    Continuous-Time Reachability

    Stephen Boyd 01:09:25