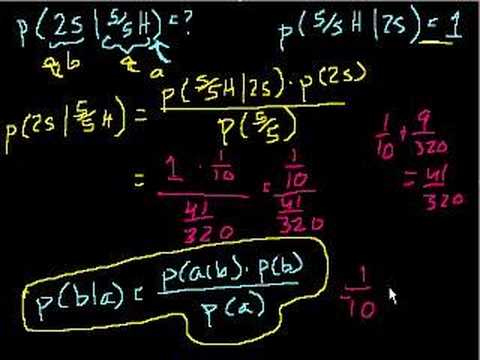Free Online Lectures and Courses for Mathematics
40 Courses
-
Precalculus
-

Introduction to Limits
-

Limit Examples (Part 1)
-

Limit Examples (Part 2)
-

Limit Examples (Part 3)
-

Squeeze Theorem
-

Proof: lim (sin x)/x
-
More Limits
-
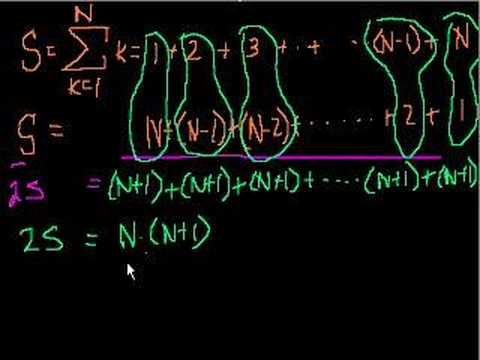
Sequences and Series Part 1
-
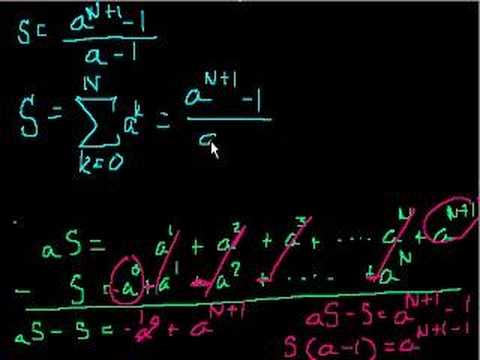
Sequences and Series Part 2
-
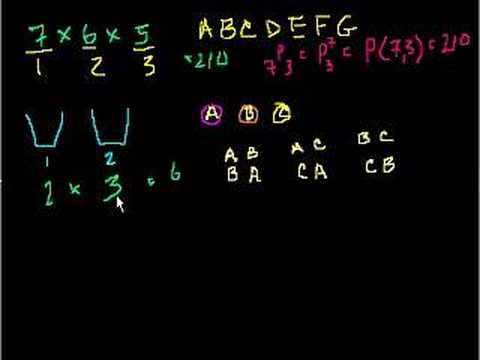
Permutations
-
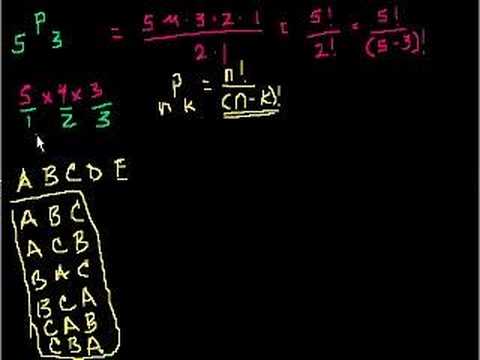
Combinations
-
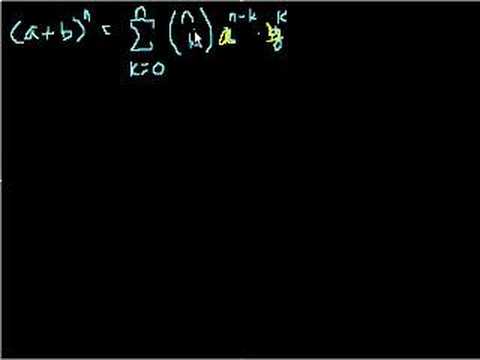
Binomial Theorem Part 1
-
Binomial Theorem Part 2
-

Binomial Theorem Part 3
-

Exponential Growth
-

Parametric Equations 1
-

Parametric Equations 2
-

Parametric Equations 3
-

Parametric Equations 4
-

Introduction to Function Inverses
-
-
Probability
-
Sequence and Series Video Tutorial
-

What is a Sequence? Basic Sequence Info
-

Sequences - Examples showing convergence or divergence
-

Summation Notation
-

What is a Series
-
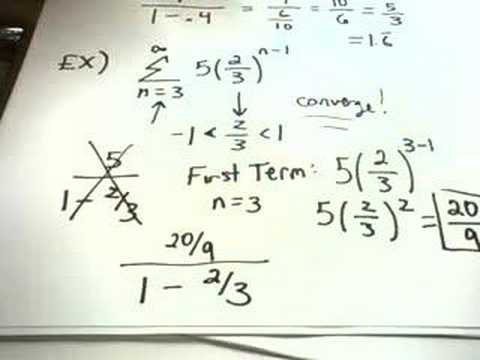
Geometric Series and the Test for Divergence - Part 1
-

Geometric Series and the Test for Divergence - Part 2
-

Geometric Series - Expressing a Decimal as a Rational Number
-

Telescoping Series Example
-
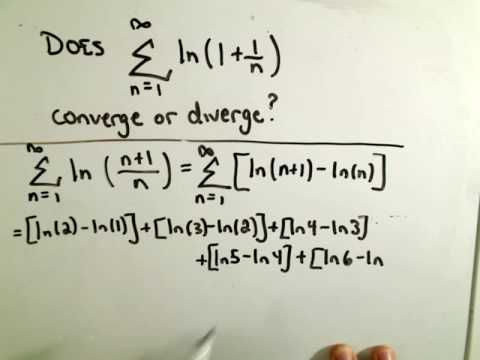
Showing a Series Diverges using Partial Sums
-
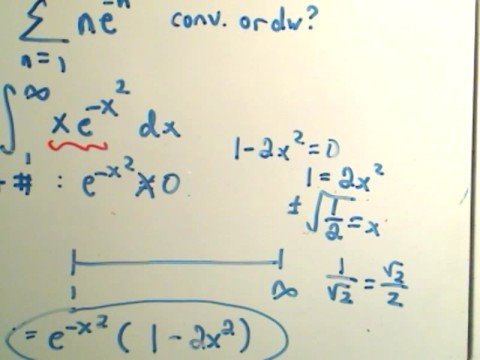
Using the Integral Test for Series
-

Remainder Estimate for the Integral Test
-

Limit Comparison Test and Direct Comparison Test (Part 1)
-

Limit Comparison Test and Direct Comparison Test (Part 2)
-

Alternating Series
-
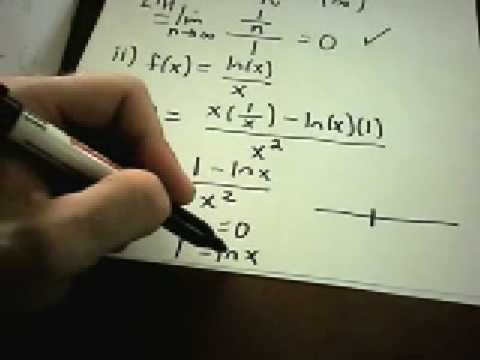
More Alternating Series Examples
-

Alternating Series Estimation Theorem
-
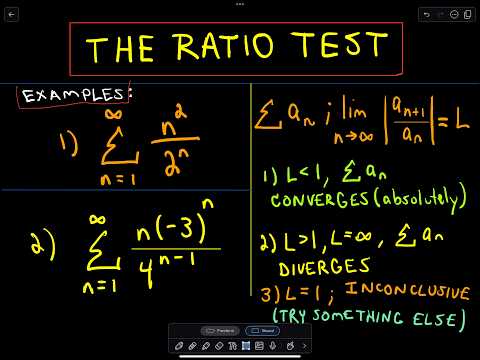
Using the Ratio Test to Determine if a Series Converges #1
-

Using the Ratio Test to Determine if a Series Converges #2
-
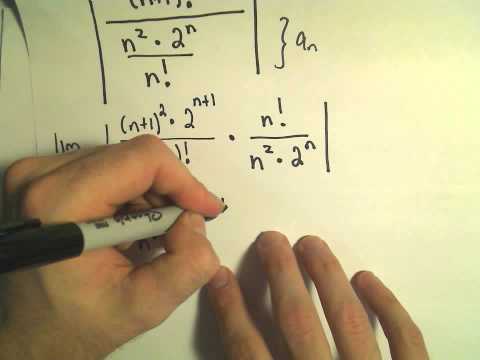
Using the Ratio Test to Determine if a Series Converges #3 (Factorials)
-

Root Test for Series
-

Strategy for Testing Series - Series Practice Problems
-

Absolute Convergence, Conditional Convergence and Divergence
-

Power Series Representation of Functions
-

Power Series - Finding the Interval of Convergence
-

Radius of Convergence for a Power Series
-

Differentiating and Integrating Power Series
-
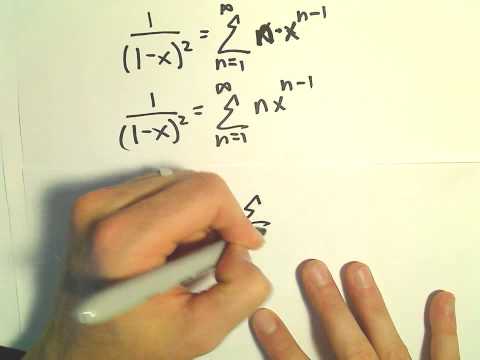
Finding the Sum of a Series by Differentiating
-

Finding Power Series by Differentiation - 3 examples
-
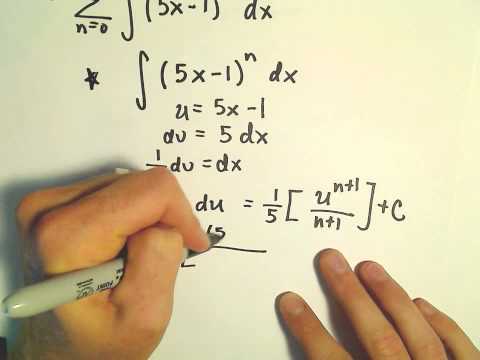
Integrating a Power Series
-

Integrating a Power Series, Example 2
-

Finding Interval of Convergence for a Given Power Series Representation
-

Interval and Radius of Convergence for a Series, Ex 3
-

Interval and Radius of Convergence for a Series, Ex 4
-

Interval and Radius of Convergence for a Series, Ex 5
-

Interval and Radius of Convergence for a Series, Ex 6
-
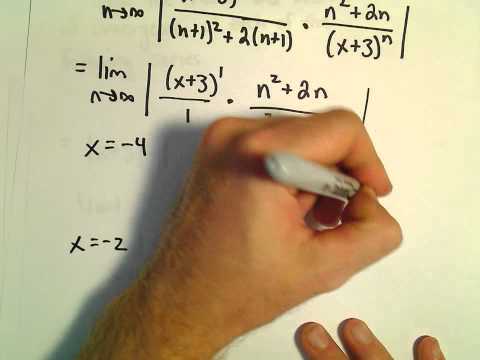
Interval and Radius of Convergence for a Series, Ex 7
-
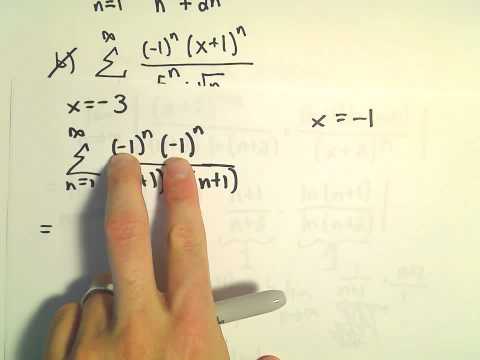
Interval and Radius of Convergence for a Series, Ex 9
-

Finding a New Power Series by Manipulating a Known Power Series
-

Finding Power Series Representations by Manipulating 1/(1-x) - Another Ex 1
-

Finding a New Power Series by Manipulating a Known Power Series, Ex 2
-
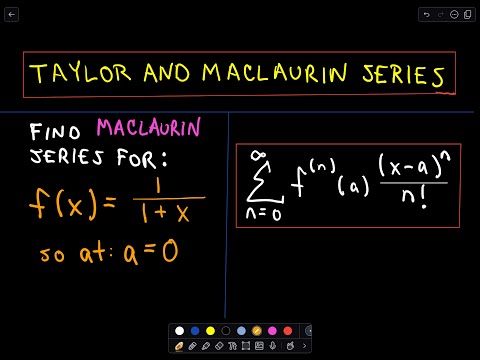
Finding a Maclaurin Series Expansion - Another Example 1
-

Taylor's Remainder Theorem - Finding the Remainder, Ex 1
-

Taylor's Remainder Theorem - Finding the Remainder, Ex 2
-
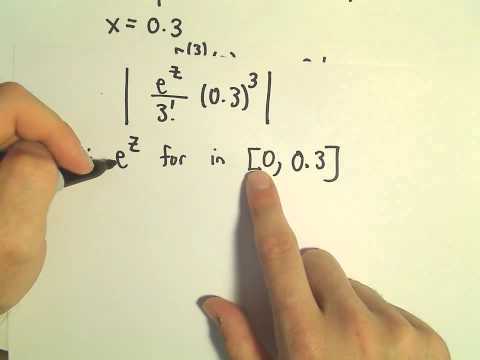
Taylor's Remainder Theorem - Finding the Remainder, Ex 3
-
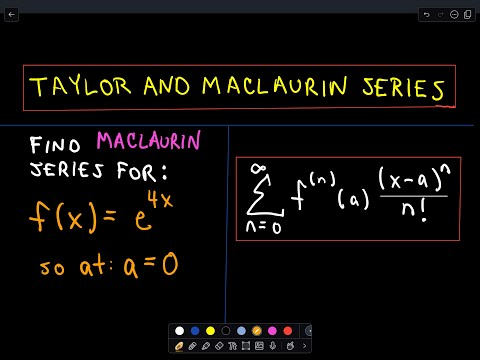
Finding a Maclaurin Polynomial - Ex 1
-
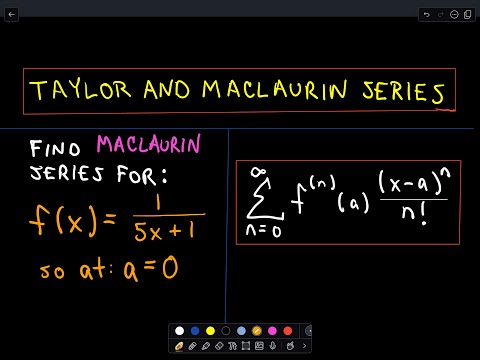
Finding a Maclaurin Polynomial - Ex 2
-

Finding a Taylor Polynomial to Approximate a Function, Ex 1
-

The Root Test - Another Example, #3
-
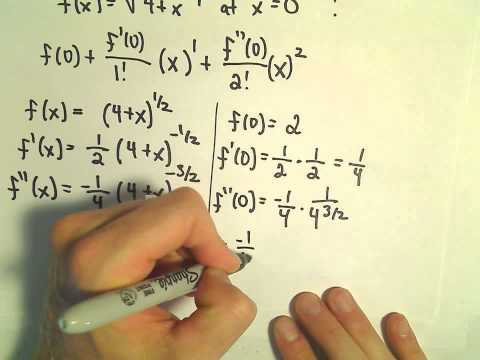
Finding a Taylor Polynomial to Approximate a Function, Ex 2
-

Finding a Taylor Polynomial to Approximate a Function, Ex 3
-
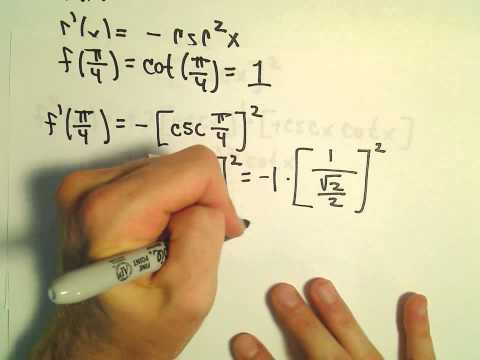
Finding a Taylor Polynomial to Approximate a Function, Ex 4
-

The Root Test - Another Example, #2
-

The Ratio Test , Another Example #1
-

The Ratio Test , Another Example #2
-

The Ratio Test , Another Example #3
-

The Ratio Test , Another Example #4
-

Absolute Convergence, Conditional Convergence, Another Example 1
-

Absolute Convergence, Conditional Convergence, Another Example 2
-

Absolute Convergence, Conditional Convergence, Another Example 3
-

Alternating Series - Another Example 1
-

Alternating Series - Another Example 2
-

Alternating Series - Another Example 3
-
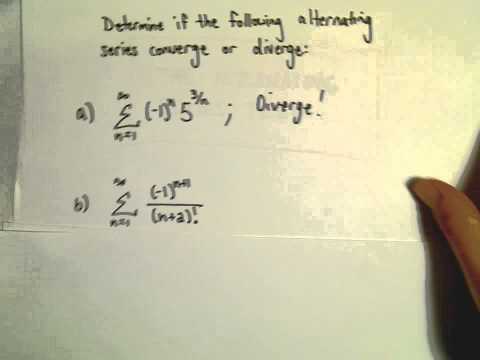
Alternating Series - Another Example 4
-

Intro to Summation Notation and Infinite Series, Ex 1
-

Limit Comparison Test for Series - Another Example 1
-

Limit Comparison Test for Series - Another Example 2
-

Limit Comparison Test for Series - Another Example 3
-

Limit Comparison Test for Series - Another Example 4
-

Limit Comparison Test for Series - Another Example 5
-

Intro to Monotonic and Bounded Sequences, Ex 1
-

The Squeeze Theorem and Absolute Value Theorem, #1
-

The Squeeze Theorem and Absolute Value Theorem, #2
-

The Squeeze Theorem and Absolute Value Theorem, #3
-

Finding the Limit of a Sequence, 3 more examples
-

Multiplication and Division of Power Series
-
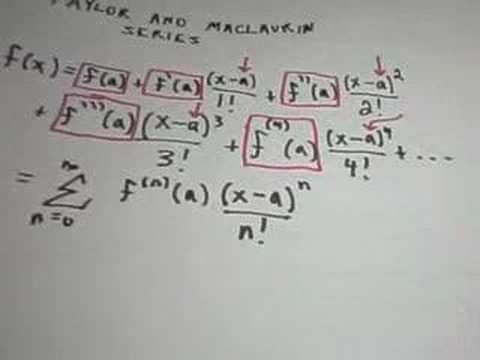
Taylor and Maclaurin Series - Example 1
-
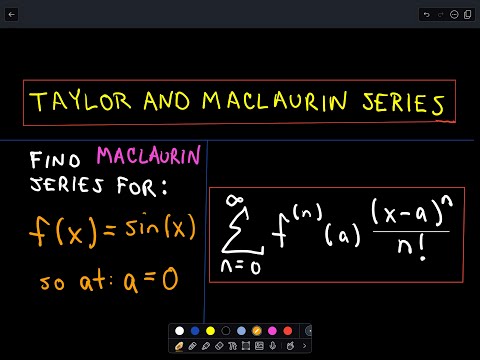
Taylor / Maclaurin Series for Sin (x)
-
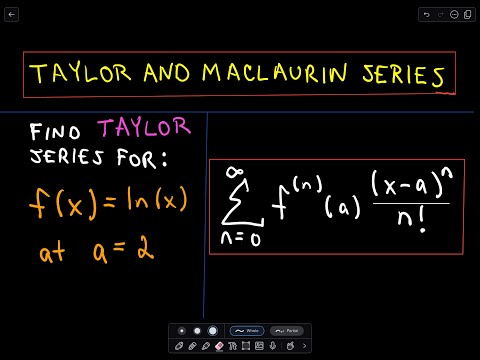
Taylor and Maclaurin Series - Example 2
-
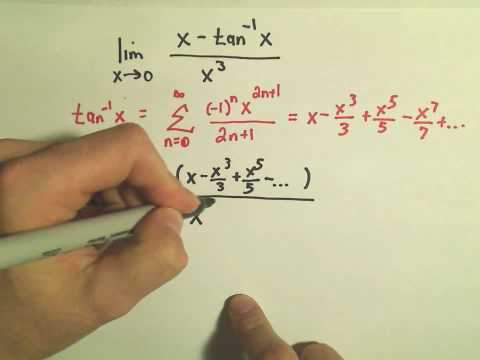
Using Series to Evaluate Limits
-
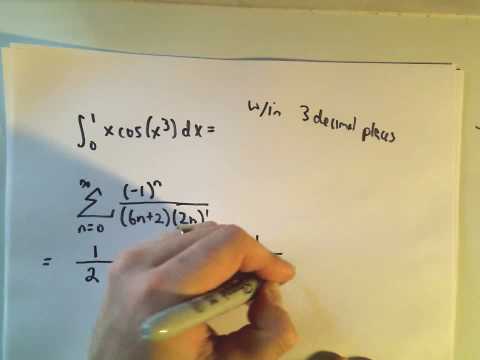
Using Maclaurin/Taylor Series to Approximate a Definite Integral
-

The Binomial Series - Example 1
-

The Binomial Series - Example 2
-

Integrating a Function as a Power Series
-
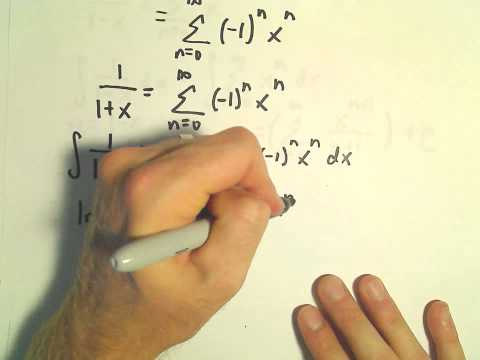
Finding a Power Series Representation for a Logarithm Function
-
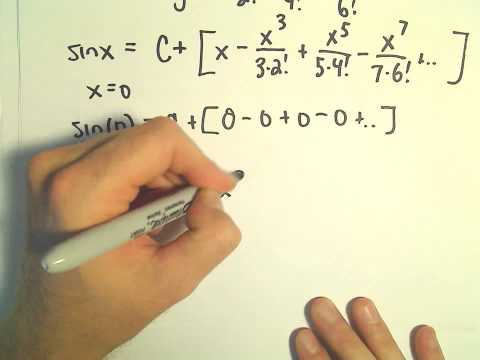
Finding a Function to Match a Given Power Series by Integrating
-
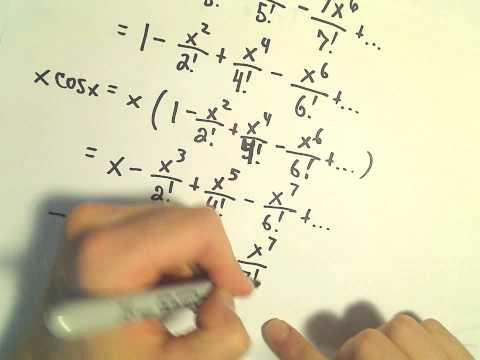
Finding a Power Series by Differentiation
-

Interval and Radius of Convergence for a Series, Ex 2
-

Direct Comparison Test - Another Example 2
-

Direct Comparison Test - Another Example 1
-

Direct Comparison Test - Another Example 3
-
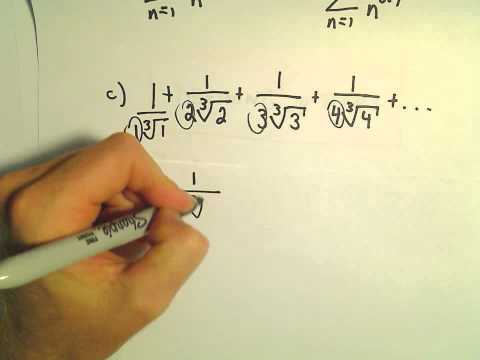
P-Series
-
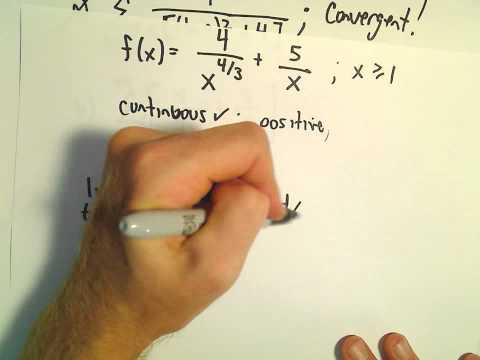
Integral Test to Evaluate Series, Ex 4
-

Integral Test to Evaluate Series, Ex 3
-
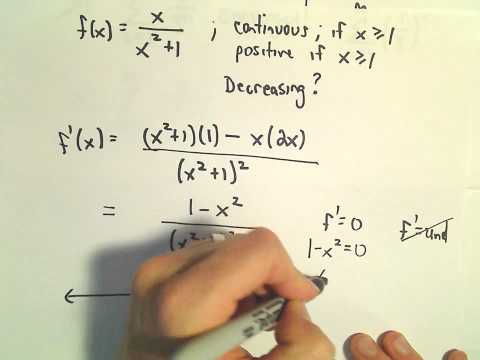
Integral Test to Evaluate Series, Ex 2
-

Integral Test to Evaluate Series, Ex 1
-

Telescoping Series ,Showing Divergence Using Partial Sums
-

Telescoping Series , Finding the Sum, Example 1
-
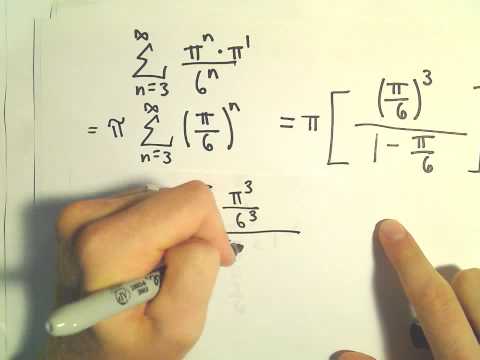
Sum of an Infinite Geometric Series, Ex 3
-

Sum of an Infinite Geometric Series, Ex 2
-

Sum of an Infinite Geometric Series, Ex 1
-

Writing a Geometric Series using Sigma / Summation Notation, Ex 2
-

Finding a Formula for a Partial Sum of a Telescoping Series
-

Writing a Geometric Series using Sigma / Summation Notation
-
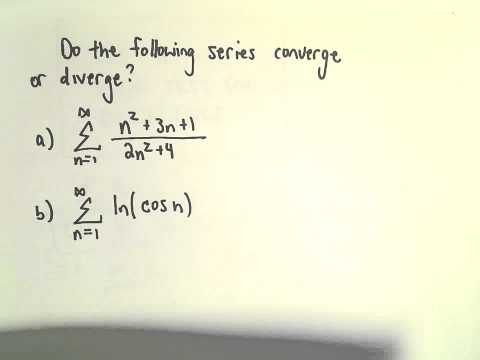
Test for Divergence for Series, Two Examples
-

Direct Comparison Test - Another Example 4
-
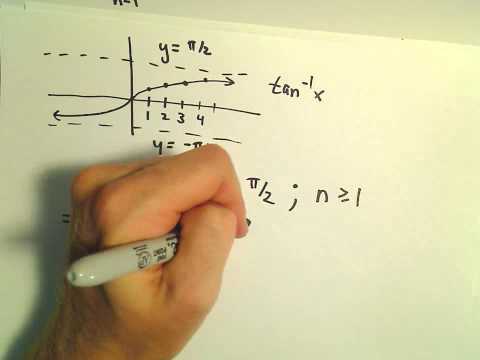
Direct Comparison Test - Another Example 5
-

The Root Test - Another Example, #1
-

Alternating Series - Error Estimation #2
-

Alternating Series - Error Estimation
-

Limit Comparison Test for Series - Another Example 6
-

Limit Comparison Test for Series - Another Example 7
-

Limit Comparison Test for Series - Another Example 8
-
-
Single Variable Calculus
-
Derivatives, Slope, Velocity, Rate of Change
-
Limits, Continuity, Trigonometric Limits
-

Derivatives of Products, Quotients, Sine, Cosine
-
Chain Rule, Higher Derivatives
-
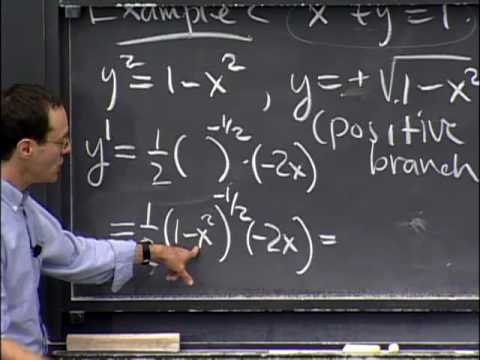
Implicit Differentiation, Inverses
-

Hyperbolic Functions (cont.) and Exam 1 Review
-

Linear and Quadratic Approximations
-
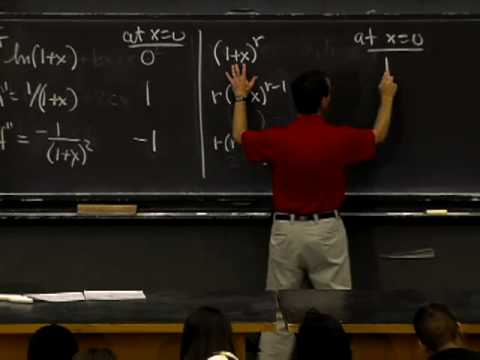
Curve Sketching
-

Max-Min Problems
-

Related Rates
-

Sets, Functions & Limits- Preface
-

Analytic Geometry
-

Inverse Functions
-

Sets, Functions & Limits- Derivatives and Limits
-

A More Rigorous Approach to Limits
-

Sets, Functions & Limits- Mathematical Inductions
-

Derivatives of Some Simple Functions
-

Approximations and Infinitesimals
-

Composite Functions and the Chain Rule
-

Differentiation of Inverse Functions
-

Implicit Differentiation
-
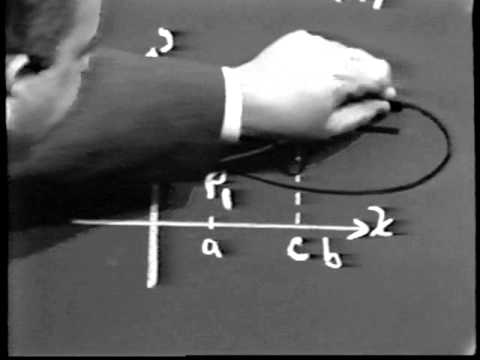
Differentiation- Continuity
-

Differentiation- Curve Plotting
-

Differentiation- Maxima and Minima
-

Differentiation- Rolle's Theorem and its Consequences
-

Differentiation- Inverse Differentiation
-

Differentiation- The "Definite" Indefinite Integral
-

The Circular Functions
-

Inverse Circular Functions
-

The Definite Integral
-

Marriage of Differential and Integral Calculus
-

Three-Dimensional Area
-

One-Dimensional Area
-

Logarithms without Exponents
-
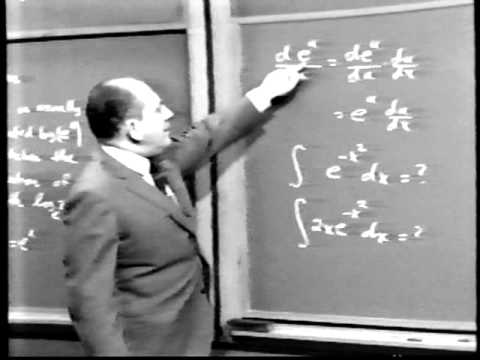
Inverse Logarithms
-

What a Difference a Sign Makes
-

Inverse Hyperbolic Functions
-

More Integration Techniques- Some Basic Recipes
-

More Integration Techniques- Partial Functions
-

More Integration Techniques- Integration by Parts
-

More Integration Techniques- Improper Integrals
-

Infinite Series- Many Versus Infinite
-

Infinite Series- Positive Series
-
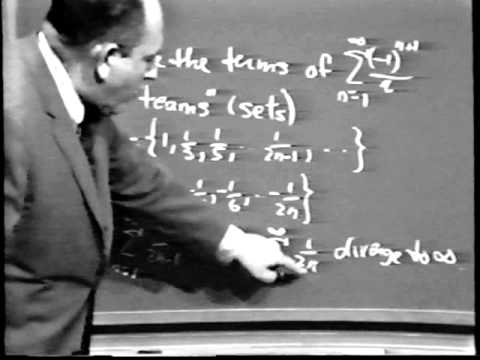
Infinite Series- Absolute Convergence
-

Infinite Series- Polynomial Approximations
-

Infinite Series- Uniform Convergence
-
-
Statistics
-

Statistics: The Average
-

Sample vs. Population Mean
-

Variance of a Population
-

Sample Variance
-

Standard Deviation
-

Alternate Variance Formulas
-

Introduction to Random Variables
-

Probability Density Functions
-
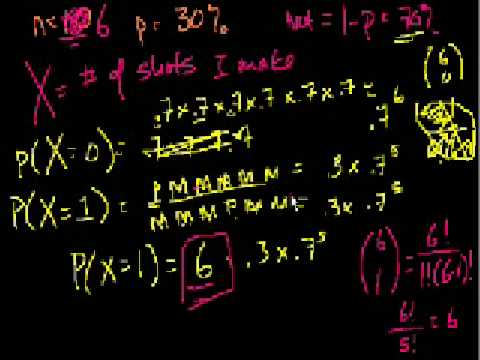
Binomial Distribution 3
-
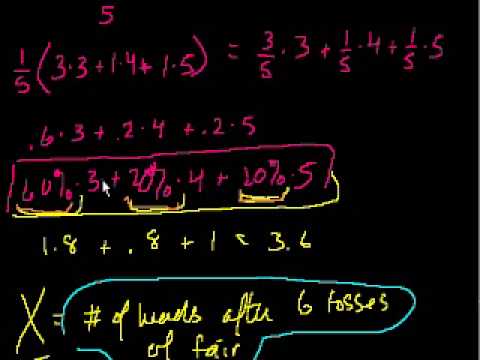
Expected Value: E(X)
-

Poisson Process 1
-

Poisson Process 2
-

Law of Large Numbers
-

Normal Distribution Excel Exercise
-
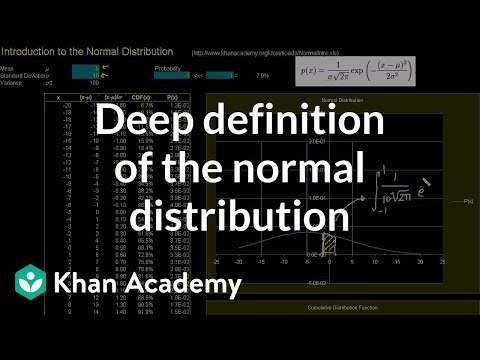
Introduction to the Normal Distribution
-

Qualitative Sense of Normal Distributions
-
Z-Score
-

Emperical Rule
-

Standard Normal Distribution and the Empirical Rule
-

More Emperical Rule and Z-Score Practice
-

Central Limit Theorem
-

Sampling Distribution of the Sample Mean Part 1
-

Sampling Distribution of the Sample Mean Part 2
-

Standard Error of the Mean
-

Sampling Distribution of the Sample Mean
-

Confidence Interval 1
-

Mean and Variance of Bernoulli Distribution Example
-

Bernoulli Distribution Mean and Variance Formulas
-

Margin of Error 1
-

Margin of Error 2
-

Confidence Interval Example
-

Small Sample Size Confidence Intervals
-

One-Tailed and Two-Tailed Tests
-

Z-statistics vs. T-statistics
-

Type 1 Errors
-

Small Sample Hypothesis Test
-

T-Statistic Confidence Interval
-

Large Sample Proportion Hypothesis Testing
-

Variance of Differences of Random Variables
-

Difference of Sample Means Distribution
-

Confidence Interval of Difference of Means
-

Clarification of Confidence Interval of Difference of Means
-

Hypothesis Test for Difference of Means
-

Comparing Population Part 1
-

Comparing Population Part 2
-

Hypothesis Test Comparing Population Proportions
-

Squared Error of Regression Line
-

Minimizing Squared Error to Regression Line Part 1
-

Minimizing Squared Error to Regression Line Part 3
-

Minimizing Squared Error to Regression Line Part 4
-

Regression Line Example
-

Minimizing Squared Error to Regression Line 2
-

R-Squared or Coefficient of Determination
-
Second Regression Example
-

Calculating R-Squared
-

Covariance and the Regression Line
-

Chi-Square Distribution Introduction
-

Pearson's Chi Square Test (Goodness of Fit)
-

Contingency Table Chi-Square Test
-

Calculating SST (Total Sum of Squares)
-

Calculating SSW and SSB (Total Sum of Squares Within and Between)
-

Hypothesis Test with F-Statistic
-
-
Statistics 110: Probability
-

Probability and Counting
-

Story Proofs, Axioms of Probability
-

Birthday Problem, Properties of Probability
-

Conditional Probability
-

Conditioning Continued, Law of Total Probability
-

Monty hall, Simpson's Paradox
-

Gambler's Ruin and Random Variables
-

Random Variables and Their Distributions
-

Expectation, Indicator Random Variables, Linearity
-

Expectation Continued
-

The Poisson Distribution
-

Discrete vs. Continuous, the Uniform
-

Normal Distribution
-

Location, Scale and LOTUS
-

Midterm Review
-

Exponential Distribution
-

Moment Generating Functions
-

Moment Generating Functions Continued
-

Joint, Conditional, and Marginal Distributions
-

Multinominal and Caucchy
-

Covariance and Correlation
-

Transformations and Convolutions
-

Beta Distribution
-

Gamma Distribution and Poisson Process
-

Order Statistics and Conditional Expectation
-

Conditional Expectation Continued
-

Conditional Expectation Given an R.V.
-

Inequalities
-

Law of Large Numbers and Central Limit Theorem
-

Chi-Square, Student-t, Multivariate Normal
-

Markov Chains
-

Markov Chains Continued
-

Markov Chains Continued Futher
-

A Look Ahead
-
-
The Fourier Transform and its Applications
-

The Fourier Series
-
Periodicity; How Sine and Cosine Can be Used to Model More Complex Functions
-
Analyzing General Periodic Phenomena as a Sum of Simple Periodic Phenomena
-

Wrapping Up Fourier Series; Making Sense of Infinite Sums and Convergence
-

Continued Discussion of Fourier Series and the Heat Equation
-

Correction to Heat Equation Discussion
-

Review of Fourier Transform (and inverse) Definitions
-
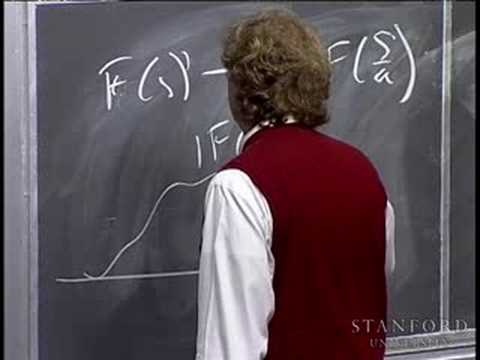
Effect on Fourier Transform of Shifting a Signal
-

Continuing Convolution: Review of the Formula
-

Central Limit Theorem and Convolution; Main Idea
-

Cop Story
-

Setting Up the Fourier Transform of a Distribution
-

Derivative of a Distribution
-

Application of the Fourier Transform: Diffraction: Setup
-

More on Results From Last Lecture (Diffraction Patterns and the Fourier Transform)
-

Review of Main Properties of the Shah Function
-

Review of Sampling and Interpolation Results
-

Aliasing Demonstration with Music
-

Review: Definition of the DFT
-
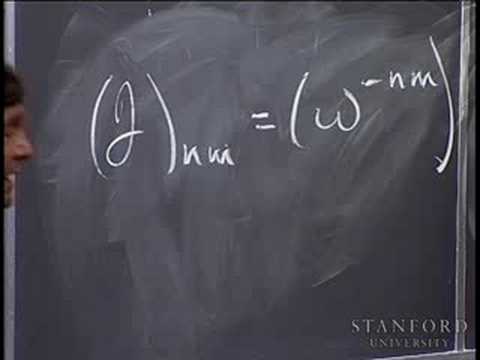
Review of Basic DFT Definitions
-

FFT Algorithm: Setup: DFT Matrix Notation
-

Linear Systems: Basic Definitions
-

Review of Last Lecture: Discrete V. Continuous Linear Systems
-
Review of Last Lecture: LTI Systems and Convolution
-

Approaching the Higher Dimensional Fourier Transform
-
Higher Dimensional Fourier Transforms- Review
-

Shift Theorem in Higher Dimensions
-

Shahs
-
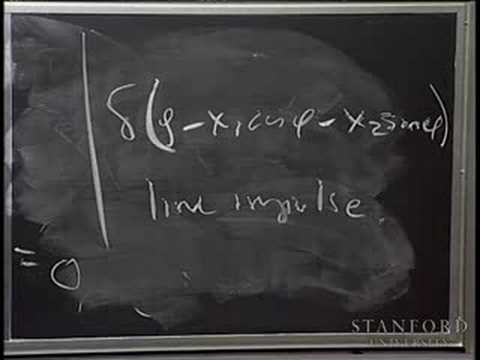
Tomography and Inverting the Radon Transform
-
-
The Mathematics of Everyday Life
-
Trigonometry
-
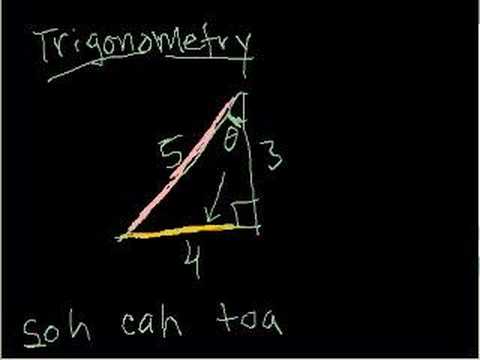
Basic Trigonometry Part 1
-
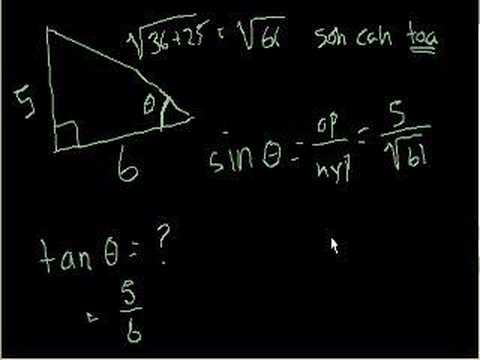
Basic Trigonometry Part 2
-

Radians and Degrees
-
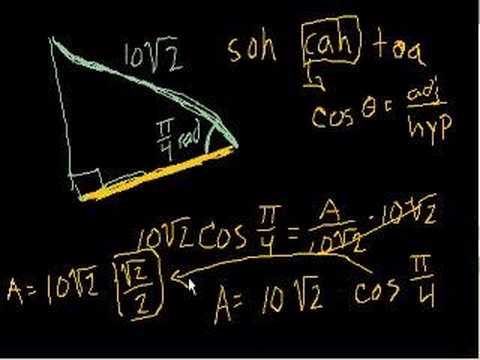
Using Trig Functions Part 1
-
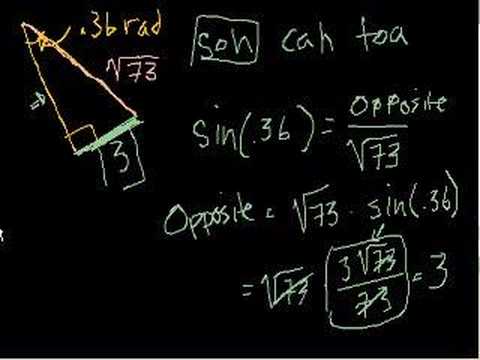
Using Trig Functions Part 2
-
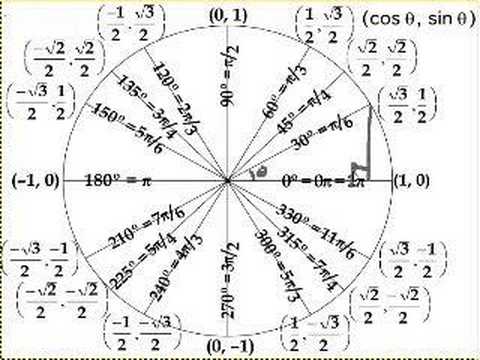
The Unit Circle Definition of Trigonometric Functions Part 1
-
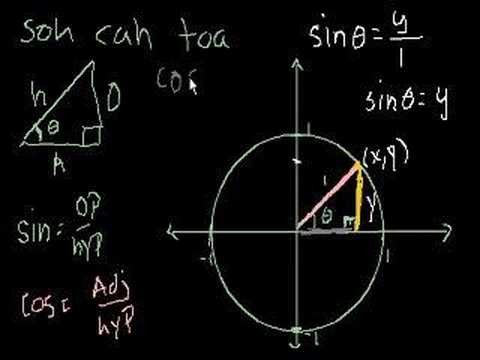
The Unit Circle Definition of Trigonometric Functions Part 2
-
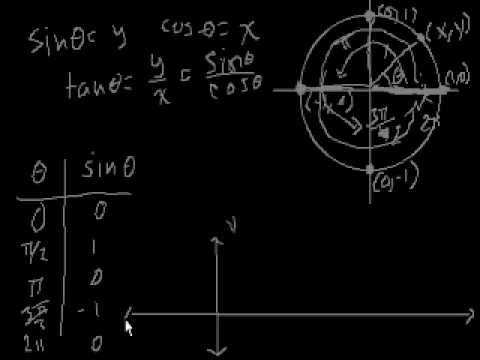
Graph of the Sine Function
-
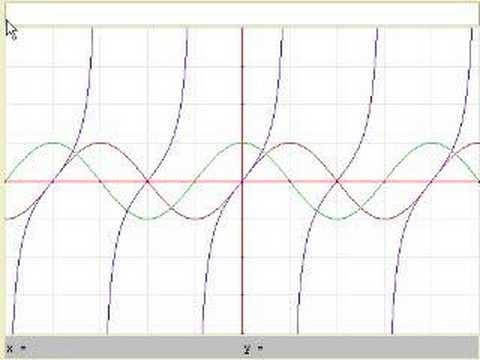
Graph of the Trig Function
-

Graphing Trig Functions
-

Trig Graphs
-
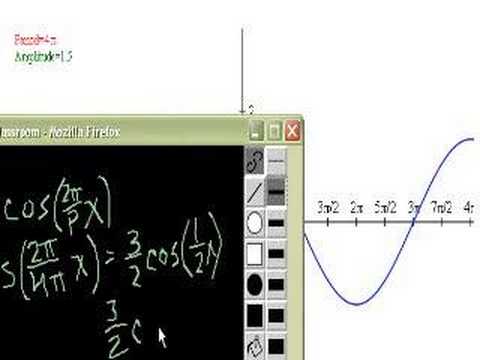
Determining the Equation of a Trigonometric Function
-

Trigonometric Identities Part 1
-
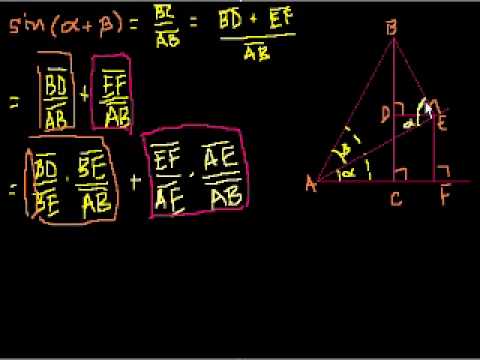
Proof: sin(a+b) = (cos a)(sin b) + (sin a)(cos b)
-
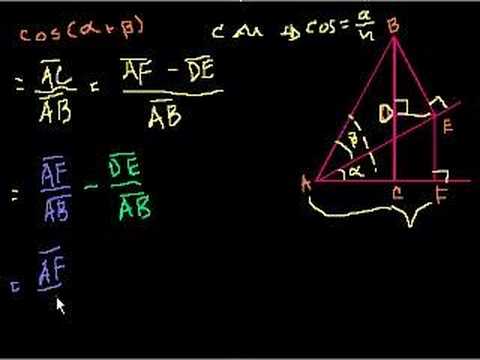
Proof: cos(a+b) = (cos a)(cos b)-(sin a)(sin b)
-

Trigonometric Identities Part 2
-

Trigonometric Identities Part 3
-
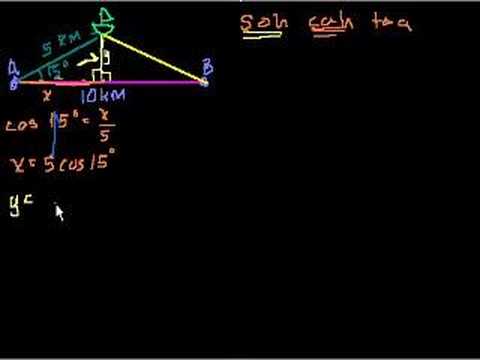
Trigonometry Word Problems Part 1
-

Trigonometry Word Problems Part 2
-

Law of Cosines
-
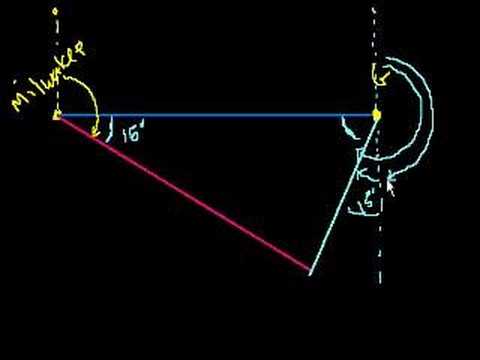
Navigation Word Problem
-

Proof: Law of Sines
-
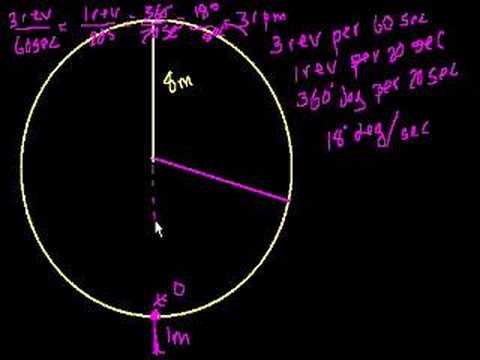
Ferris Wheel Trig Problem Part 1
-
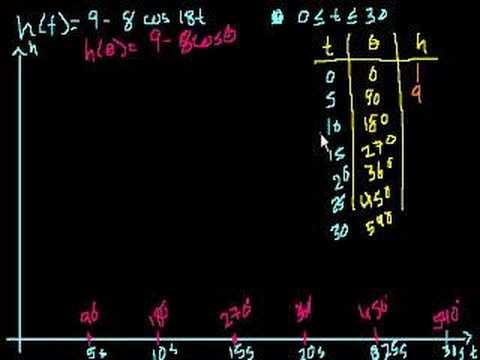
Ferris Wheel Trig Problem Part 2
-
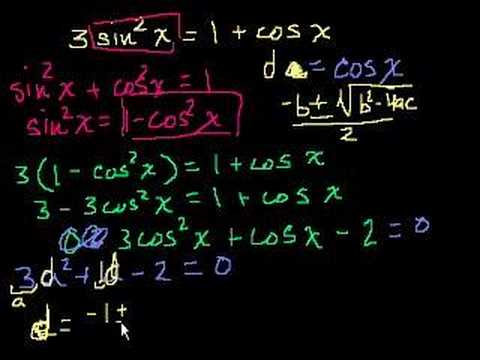
Fun Trig Problem
-

Inverse Trig Functions: Arcsin
-

Inverse Trig Functions: Arctan
-

Inverse Trig Functions: Arccos
-

Trigonometry Identity Review/Fun
-
-
Vector Calculus
-

Applications of Double Integrals
-

Path Integrals - How to Integrate Over Curves
-

Vector Fields
-

Divergence
-

Curl
-

Line Integrals (2)
-

Applications of Line Integrals
-

Fundamental Theorem of Line Integrals
-

Green's Theorem
-

More on Green's Theorem
-
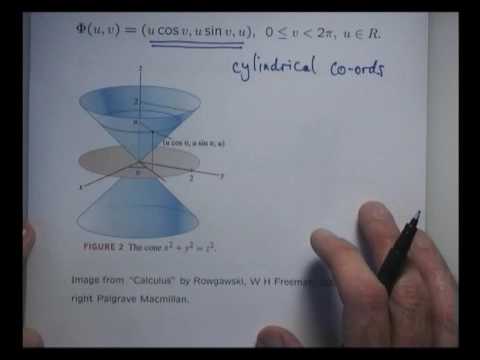
Parametrised Surfaces
-

Surface Integrals
-

More on Surface Integrals
-

Surface Integrals and Vector Fields
-

Partial Differential Equations
-

Separable Differential Equations
-