Free Online Lectures and Courses for Mathematics
40 Courses
-
Algebra
-

Simple Equations
-

Equations Part 2
-

Equations Part 3
-

Linear Equations
-

Graphing Lines Part 1
-
Slope and Y-intercept Intuition
-

Slope Part 1
-
Slope Part 2
-
Slope Part 3
-

Averages
-

Integer Sums
-

Taking Percentages
-
Growing by a Percentage
-

Another Percent Word Problem
-

More Percent Problems
-

Systems of Equations
-

Ratio Problem with Basic Algebra
-

Ratio Problem: Advanced
-

Alternate Solution to Ratio Problem
-

Introduction to Ratios
-
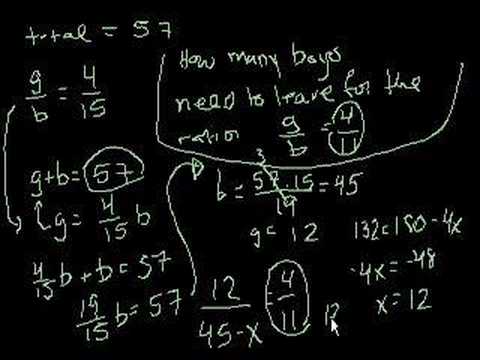
Advanced Ratio Problems
-

Age Word Problems Part 1
-

Age Word Problems Part 2
-

Age Word Problems Part 3
-

Level 1 Multiplying Expressions
-

Solving a Quadratic by Factoring
-
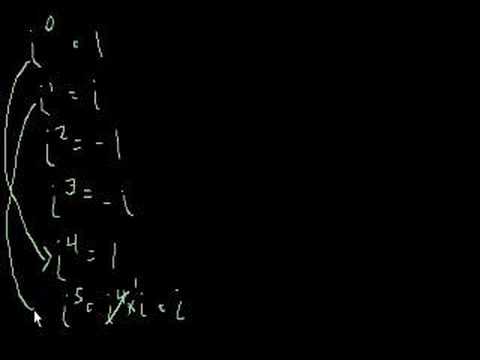
i and Imaginary Numbers
-
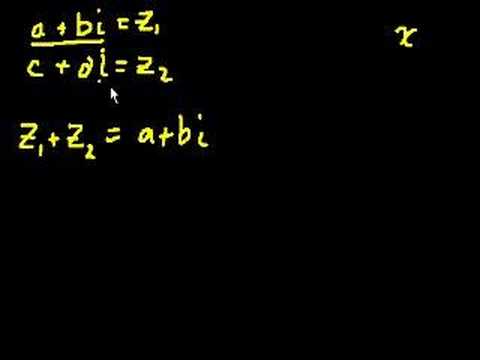
Complex Numbers Part 1
-
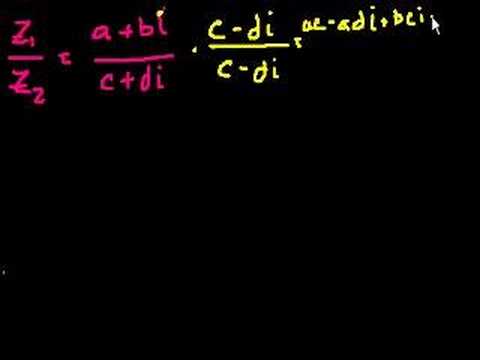
Complex Numbers Part 2
-

Introduction to the Quadratic Equation
-

Quadratic Equation Part 2
-
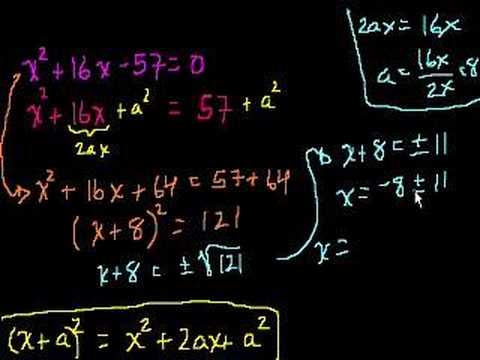
Completing the Square
-

Quadratic Formula
-

Quadratic Inequalities
-
Functions Part 1
-
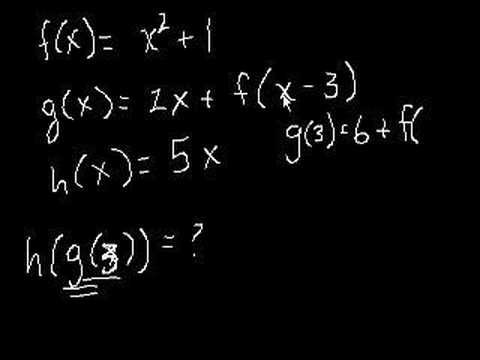
Functions Part 2
-
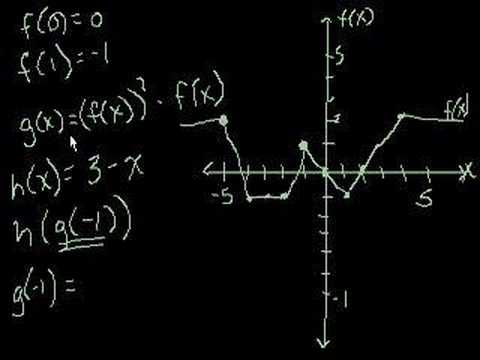
Functions Part 3
-
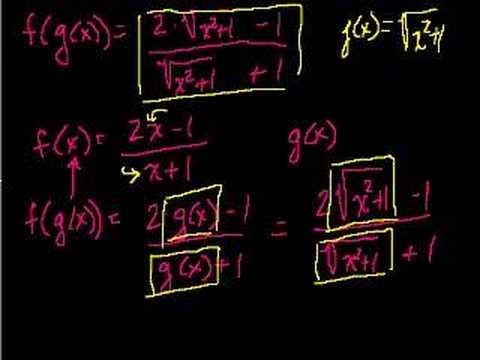
Functions Part 4
-

Domain of a Function
-

Proof: log a + log b = log ab
-

Proof: A(log B) = log (B^A), log A - log B = log (A/B)
-
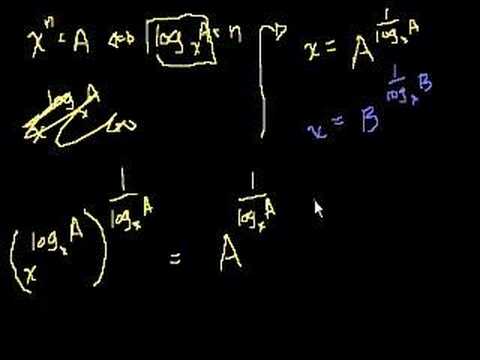
Proof: log_a (B) = (log_x (B))/(log_x (A))
-
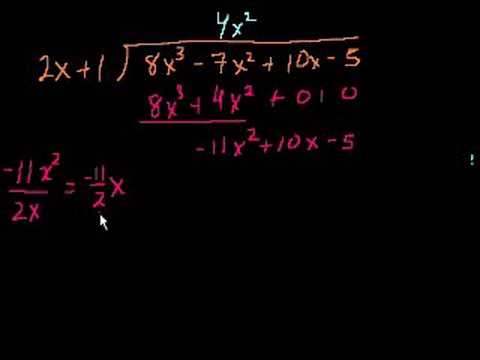
Algebraic Long Division
-

Introduction to Conic Sections
-
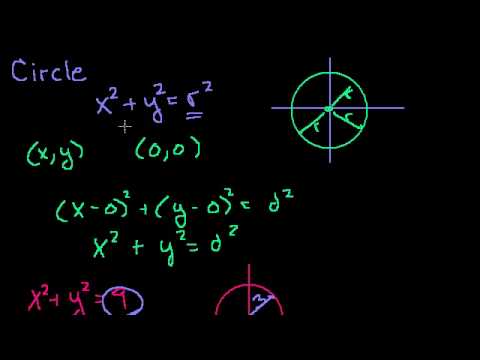
Conic Sections: Circles
-

Conic Sections: Ellipses
-

Conic Sections: Hyperbolas Part 1
-

Conic Sections: Hyperbolas Part 2
-

Conic Sections: Hyperbolas Part 3
-

Identifying Conics Part 1
-

Identifying Conics Part 2
-

Identifying Conics Part 3
-

Foci of an Ellipse
-

Foci of a Hyperbola
-

Hyperbola Foci
-

Partial Fraction Expansion Part 1
-

Partial Fraction Expansion Part 2
-

Partial Fraction Expansion Part 3
-
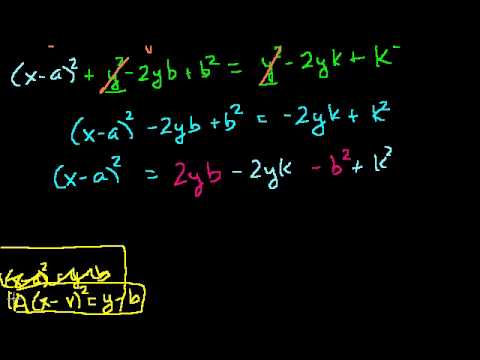
Parabola Focus and Directrix Part 1
-
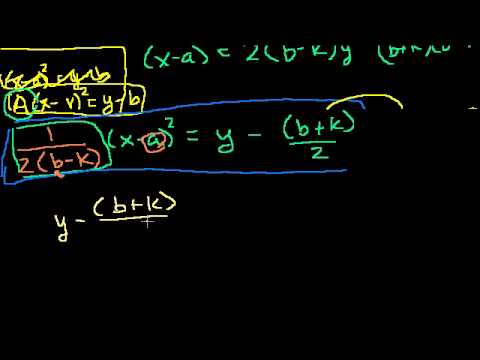
Parabola Focus and Directrix Part 2
-

Two Passing Bicycles Word Problem
-

Passed Bike Word Problem
-

Passing Trains
-
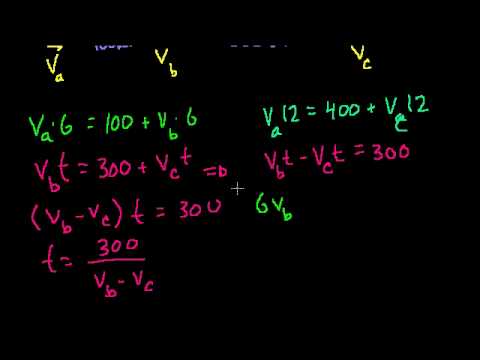
Overtaking Word Problem
-

Early Train Word Problem
-

Officer on Horseback
-

Rational Inequalities Part 1
-

Rational Inequalities Part 2
-
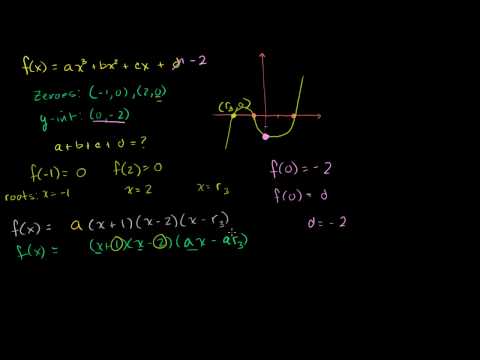
Interesting Polynomial
-

Geometric Series Sum to Figure Out Mortgage Payments
-
-
Algebra I Worked Examples
-

Solving Equations 1
-

Solving Equations 2
-

Solving Equations with the Distributive Property
-

Solving Equations with the Distributive Property 2
-

Algebraic Word Problem
-

Sum of Consecutive Odd Integers
-

Example of Solving for a Variable
-

Solving for a Variable 2
-

Absolute Value 1
-

Absolute Value and Number Lines
-

Absolute Value Equations 1
-

Absolute Value Equations 2
-

Patterns in Sequences 1
-

Patterns in Sequences 2
-

Equations of Sequence Patterns
-

Finding the 100th Term in a Sequence
-

Functional Relationships 1
-

Testing if a Relationship is a Function
-

Domain and Range 1
-

Domain and Range 2
-

Direct Variation 1
-

Basic Rate Problem
-

Basic Linear Function
-

Exploring Linear Relationships
-

Recognizing Linear Functions
-
Exploring Nonlinear Relationships
-
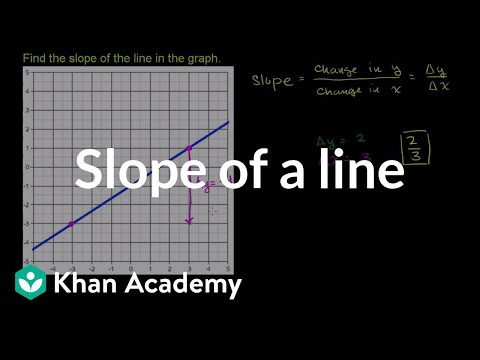
Slope of a Line
-

Slope Example
-

X and Y Intercepts
-

X and Y Intercepts 2
-

Graphing a Line in Slope Intercept Form
-
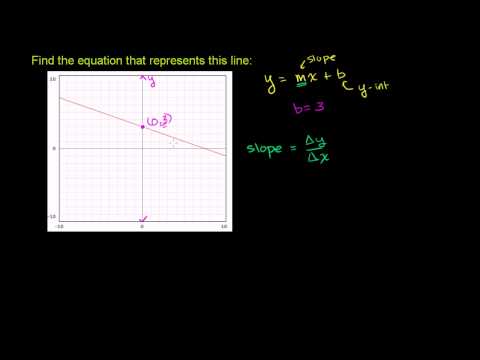
Equation of a Line
-
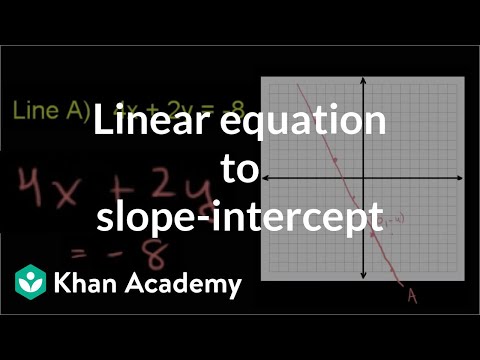
Converting to Slope Intercept Form
-

Point-slope and Standard Form
-

Parallel Lines 1
-

Parallel Lines 2
-

Parallel Lines 3
-

Perpendicular Lines 1
-

Perpendicular Lines 2
-

Interpreting Inequalities
-

Solving Inequalities
-

Inequalities
-

Absolute Value Inequalities
-

Absolute Inequalites 2
-

Absolute Value Inequalities 3
-

Writing and Using Inequalities 1
-

Writing and Using Inequalities 2
-

Writing and Using Inequalities 3
-

Solving and Graphing Linear Inequalities in Two Variables
-
Graphing Linear Inequalities in Two Variables 1
-

Graphing Linear Inequalities in Two Variables 2
-
Solving Systems By Graphing 1
-

Solving Systems By Graphing 2
-

Solving Systems By Graphing 3
-

Solving Systems By Substitution 1
-

Solving Systems By Substitution 2
-

Solving Systems By Substitution 3
-

Solving Systems By Elimination 1
-

Solving Systems By Elimination 2
-

Solving Systems By Elimination 3
-

Systems and Rate Problems 1
-

Systems and Rate Problems 2
-

Systems and Rate Problems 3
-

Mixture Problems 1
-

Mixture Problems 2
-

Mixture Problems 3
-
Graphing Systems of Inequalities 1
-

Graphing Systems of Inequalities 2
-

Graphing Systems of Inequalities 3
-

Exponent Rules 1
-
Exponent Rules 2
-

Exponent Rules 3
-

Scientific Notation 1
-

Scientific Notation 2
-

Scientific Notation 3
-

Simplifying Expressions with Exponents 1
-

Simplifying Expressions with Exponents 2
-

Simplifying Expressions with Exponents 3
-

Pythagorean Theorem 1
-

Pythagorean Theorem 2
-
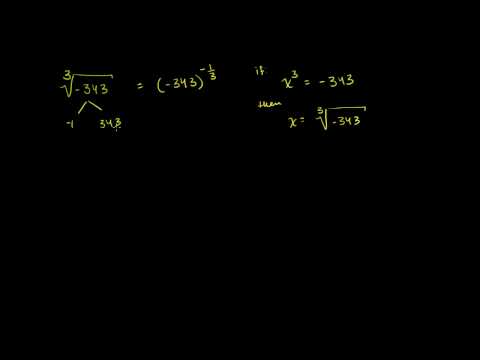
Simplifying Radical Expressions 1
-
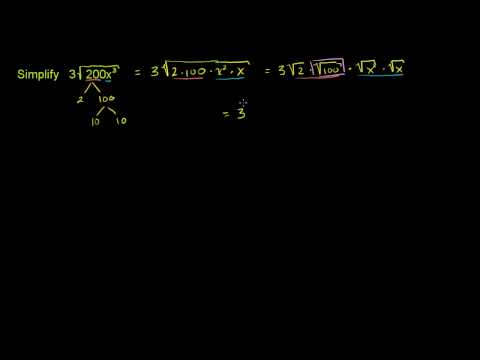
Simplifying Radical Expressions 2
-
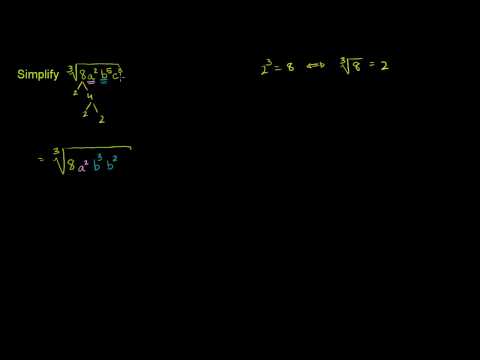
Simplifying Radical Expressions 3
-

Solving Radical Expressions 1
-

Solving Radical Expressions 2
-

Solving Radical Expressions 3
-

Applying Radical Equations 1
-

Applying Radical Equations 2
-

Applying Radical Equations 3
-

Fractional Exponent Expressions 1
-

Fractional Exponent Expressions 2
-

Multiplying and Dividing Monomials 1
-

Multiplying and Dividing Monomials 2
-

Multiplying and Dividing Monomials 3
-

Polynomials 1
-

Polynomials 2
-

Adding and Subtracting 1
-

Adding and Subtracting 2
-

Adding and Subtracting 3
-

Multiplying Polynomials 1
-

Multiplying Polynomials 2
-

Multiplying Polynomials 3
-

Special Products of Polynomials 1
-
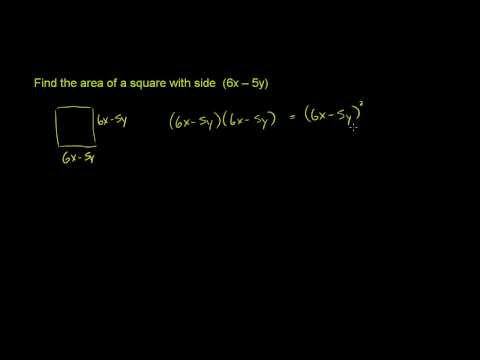
Special Products of Polynomials 2
-
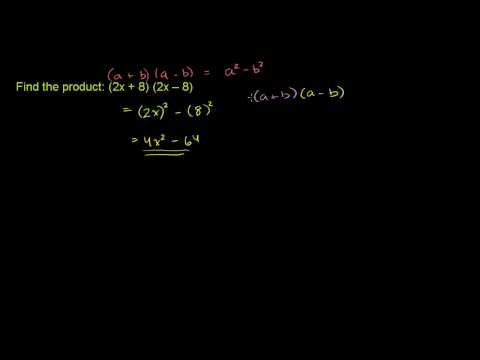
Special Products of Polynomials 3
-
Bay Area CBS Station with Slaman Khan
-

Factoring and the Distributive Property 1
-

Factoring and the Distributive Property 2
-

Factoring and the Distributive Property 3
-

Factoring Trinomials By Grouping 1
-
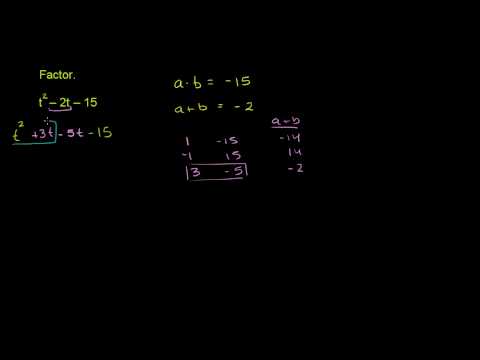
Factoring Trinomials By Grouping 2
-
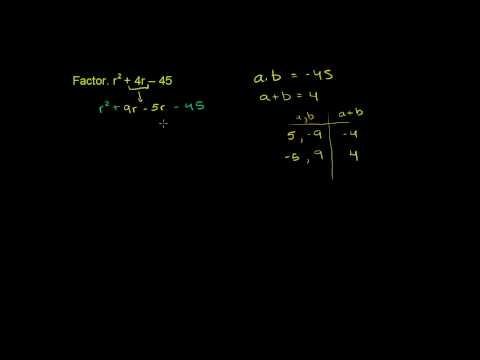
Factoring Trinomials By Grouping 3
-

Factoring Trinomials By Grouping 4
-

Factoring Trinomials By Grouping 5
-

Factoring Trinomials by Grouping 6
-

Factoring Special Products 1
-

Factoring Special Products 2
-

Factoring Special Products 3
-

Solving Quadratic Equations By Factoring 1
-

Solving Quadratic Equations By Factoring 2
-

Solving Quadratic Equations By Factoring 3
-
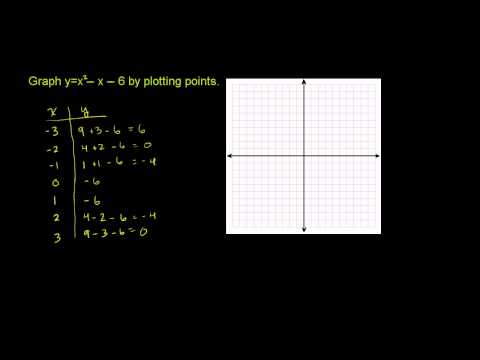
Quadratic Functions 1
-

Quadratic Functions 2
-

Quadratic Functions 3
-

Completing the Square 1
-

Completing the Square 2
-

Completing the Square 3
-

Completing the Square 4
-

Quadratic Formula 1
-

Quadratic Formula 2
-

Quadratic Formula 3
-
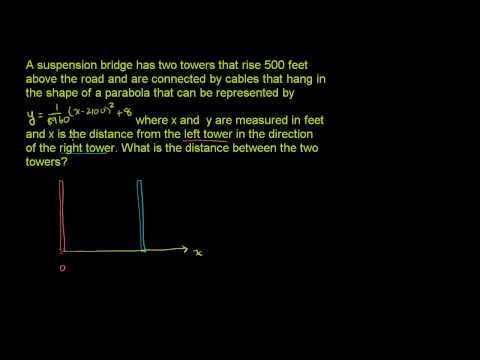
Applying Quadratic Functions 1
-

Applying Quadratic Functions 2
-

Applying Quadratic Functions 3
-

Non-Linear Systems of Equations 1
-

Non-Linear Systems of Equations 2
-

Non-Linear Systems of Equations 3
-

Simplifying Rational Expressions 1
-

Simplifying Rational Expressions 2
-

Simplifying Rational Expressions 3
-

Multiplying and Dividing Rational Expressions 1
-

Multiplying and Dividing Rational Expressions 2
-

Multiplying and Dividing Rational Expressions 3
-

Adding and Subtracting Rational Expressions 1
-

Adding and Subtracting Rational Expressions 2
-

Adding and Subtracting Rational Expressions 3
-

Solving Rational Equations 1
-

Solving Rational Equations 2
-

Solving Rational Equations 3
-

Applying Rational Equations 1
-

Applying Rational Equations 1 Extra
-

Applying Rational Equations 2
-

Applying Rational Equations 3
-
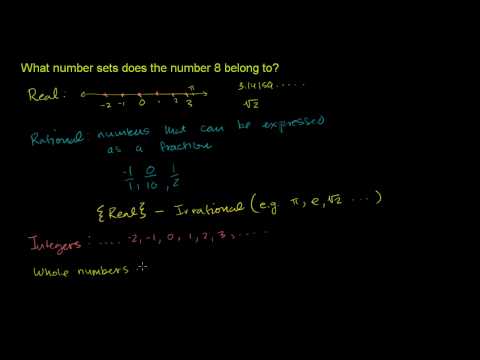
Number Sets 1
-

Number Sets 2
-

Number Sets 3
-

Understanding Logical Statements 1
-
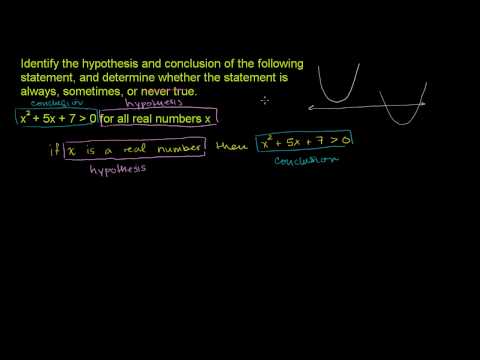
Understanding Logical Statements 2
-

Understanding Logical Statements 3
-
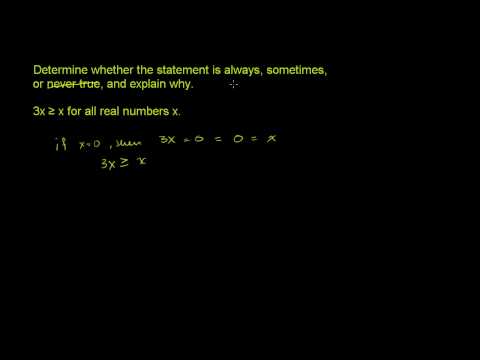
Understanding Logical Statements 4
-

Understanding Logical Statements 5
-

Inductive Reasoning 1
-

Inductive Reasoning 2
-

Inductive Reasoning 3
-

Deductive Reasoning 1
-

Deductive Reasoning 2
-

Deductive Reasoning 3
-

Events and Outcomes 1
-
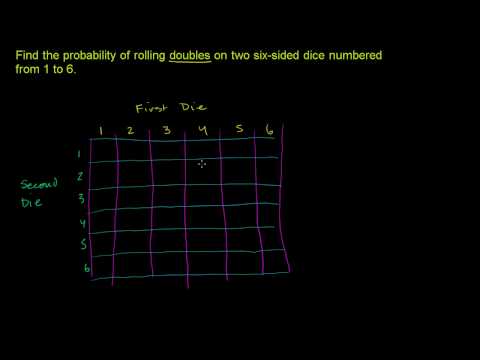
Events and Outcomes 2
-

Events and Outcomes 3
-

Independent Events 1
-

Independent Events 2
-

Independent Events 3
-

Permutations and Combinations 1
-

Permutations and Combinations 2
-

Permutations and Combinations 3
-

Permutations and Combinations 4
-

Probability of Dependent Events 1
-

Probability of Dependent Events 2
-

Absolute Value Equations
-

Graphing Systems of Inequalities
-
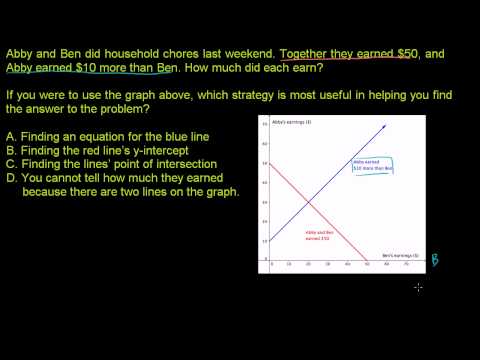
Solving Systems By Graphing
-
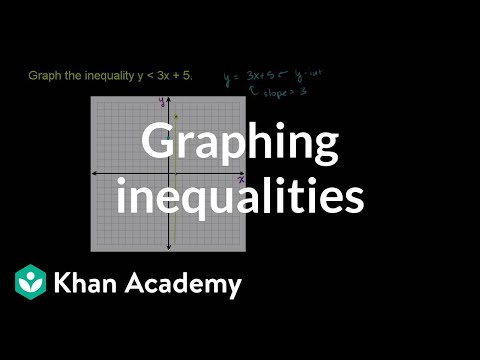
Graphing Linear Inequalities in Two Variables
-

Representing Functions as Graphs
-

Inductive Patterns
-
-
Arithmetic
-

Basic Addition
-

Addition 2
-

Level 2 Addition
-

Addition 3
-

Addition 4
-

Basic Subtraction
-

Subtraction 2
-

Subtraction 3: Introduction to Borrowing or Regrouping
-

Alternate Mental Subtraction Method
-
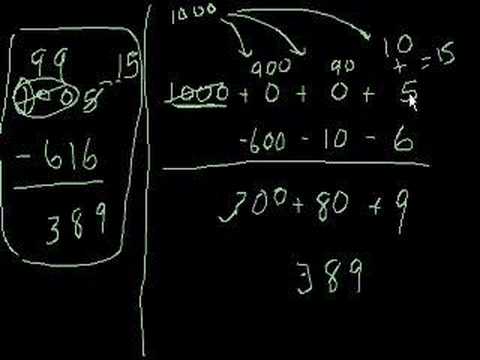
Why Borrowing Works
-
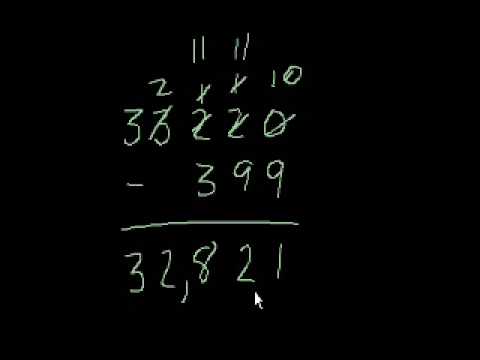
Level 4 Subtraction
-
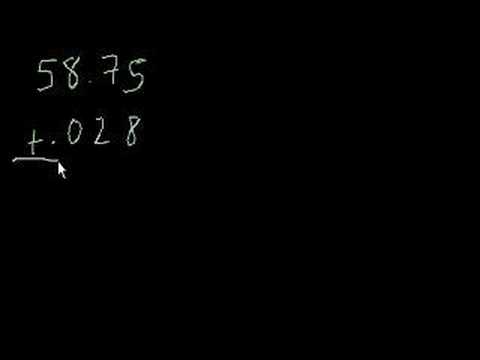
Adding Decimals
-

Subtracting Decimals
-

Basic Multiplication
-

Multiplication 2: The Multiplication Tables
-

Multiplication 3: 10,11,12 Times Tables
-

Multiplication 4: 2-digit Times 1-digit Number
-

Multiplication 5: 2-digit Times a 2-digit Number
-

Multiplication 6: Multiple Digit Numbers
-

Multiplication 7: Old Video Giving More Examples
-

Mulitplication 8: Multiplying Decimals (Old video)
-

Lattice Multiplication
-

Why Lattice Multiplication Works
-

Division 1
-

Division 2
-

Division 3: More Long Division and Remainder Examples
-

Level 4 Division
-

Converting Fractions to Decimals
-
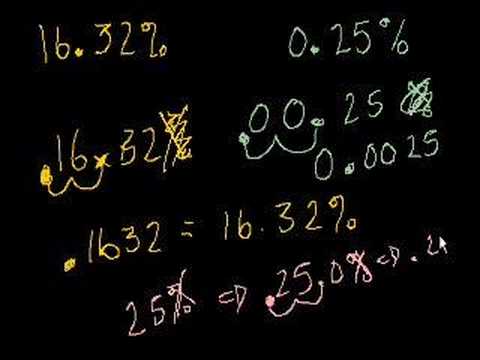
Percent and Decimals
-

Dividing Decimals
-

Ordering Numeric Expressions
-

Greatest Common Divisor
-

Least Common Multiple
-

Equivalent Fractions
-

Mixed Numbers and Improper Fractions
-
-
Calculus
-

Epsilon Delta Limit Definition Part 1
-

Epsilon Delta Limit Definition Part 2
-

Calculus: Derivatives 1
-

Calculus: Derivatives 2
-

Calculus: Derivatives 2.5
-

Derivatives Part 1
-

Derivatives Part 2
-

Derivatives Part 3
-

Derivatives Part 4
-
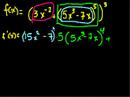
Derivatives Part 5
-
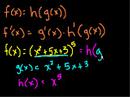
Derivatives Part 6
-

Derivatives Part 7
-

Derivatives Part 8
-

Derivatives Part 9
-

Proof: d/dx(x^n)
-

Proof: d/dx(sqrt(x))
-

Proof: d/dx(ln x) = 1/x
-

Proof: d/dx(e^x) = e^x
-

Proofs of Derivatives of Ln(x) and e^x
-

Extreme Derivative Word Problem
-

Implicit Differentiation Part 1
-
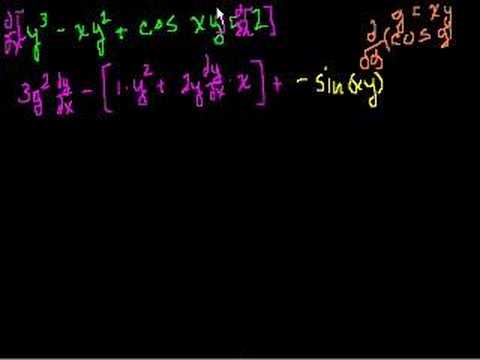
Implicit Differentiation Part 2
-
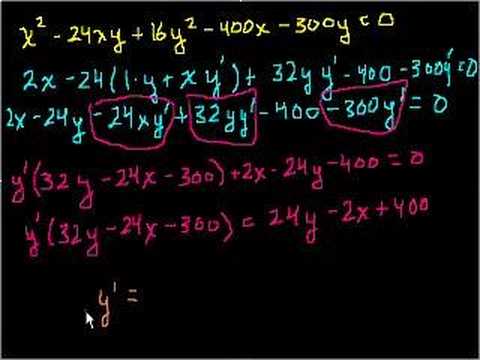
More Implicit Differentiation
-
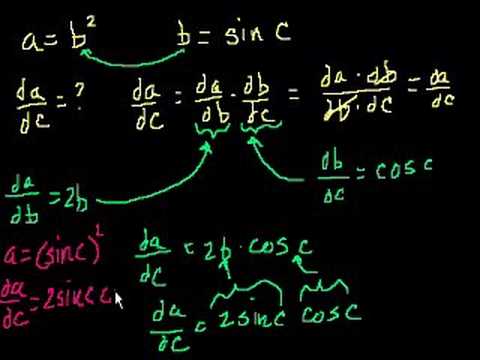
More Chain Rule and Implicit Differentiation Intuition
-
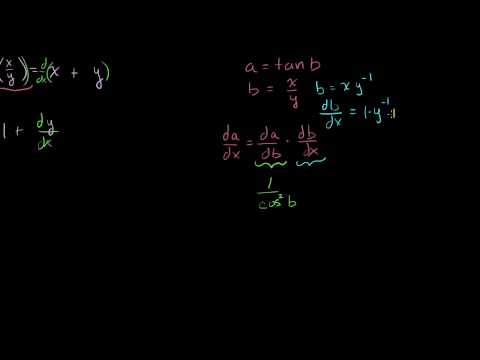
Trig Implicit Differentiation Example
-

Derivative of x^(x^x)
-
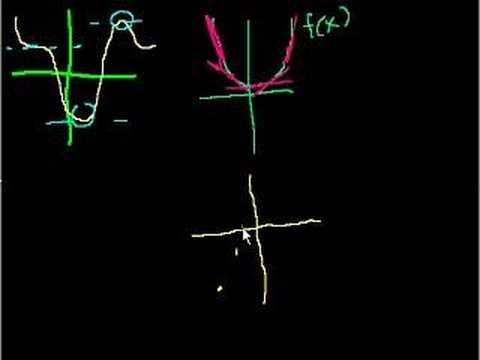
Maxima Minima Slope Intuition
-

Inflection Points and Concavity Intuition
-
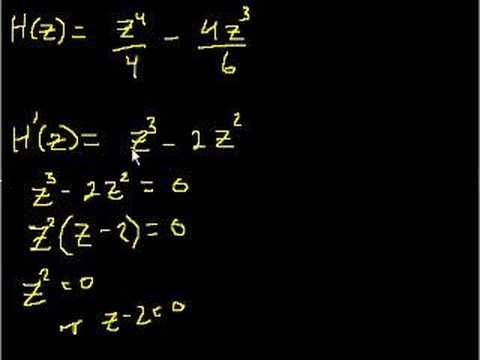
Monotonicity Theorem
-

Maximum and Minimum Values on an Interval
-

Graphing Using Derivatives
-

Graphing with Derivatives Example
-

Graphing with Calculus
-
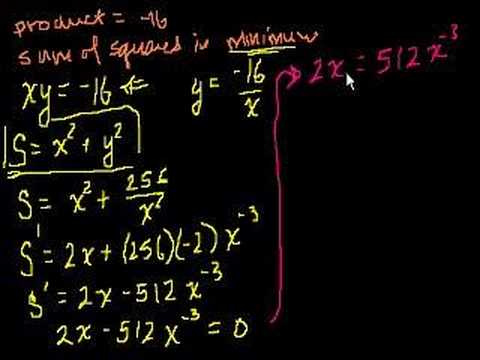
Optimization with Calculus Part 1
-
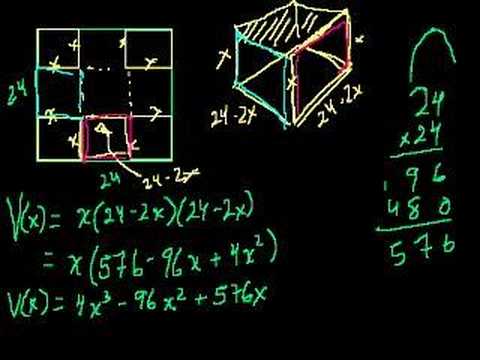
Optimization with Calculus Part 2
-

Optimization with Calculus Part 3
-

Optimization with Calculus Part 4
-
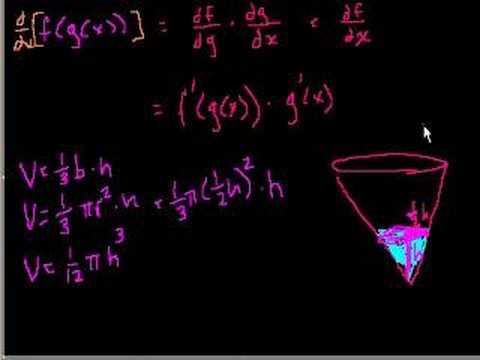
Introduction to Rate-of-change
-

Equation of a Tangent Line
-
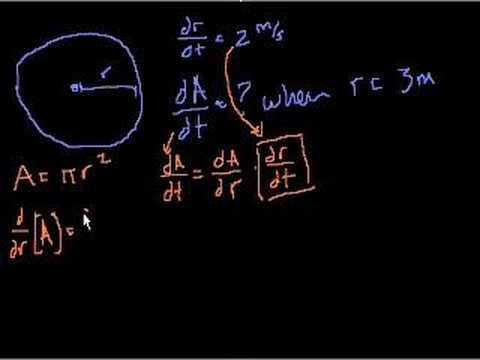
Rates-of-change Part 2
-
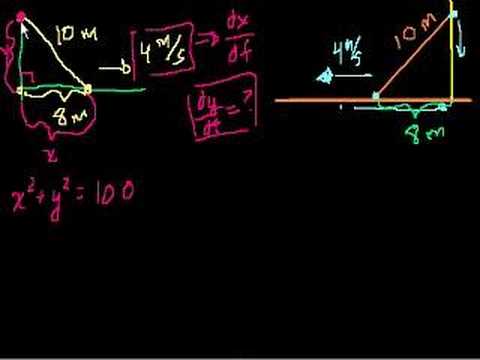
Ladder rate-of-change Problem
-

Mean Value Theorem
-

Indefinite Integrals Part 1
-
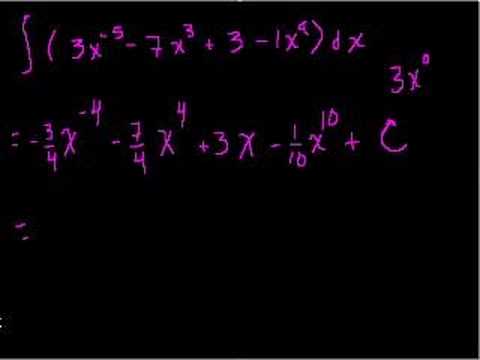
Indefinite Integrals Part 2
-
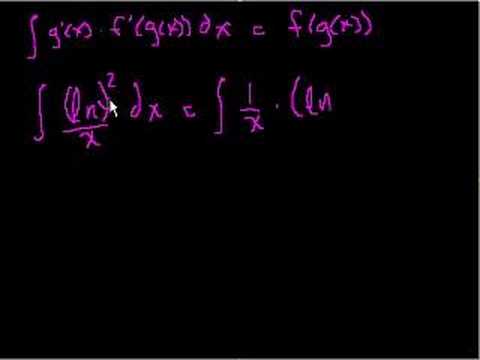
Indefinite Integrals Part 3
-
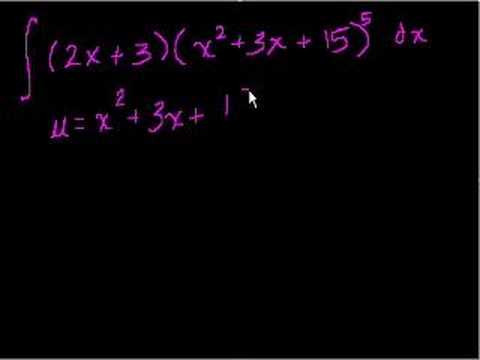
Indefinite Integrals Part 4
-

Indefinite Integrals Part 5
-
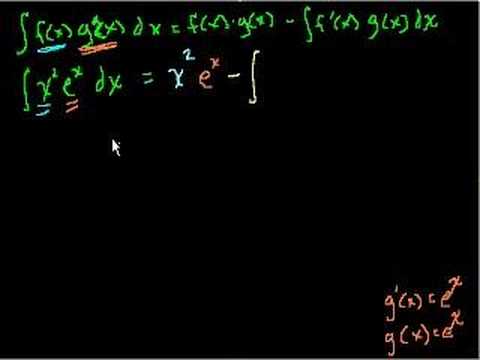
Indefinite Integrals Part 6
-
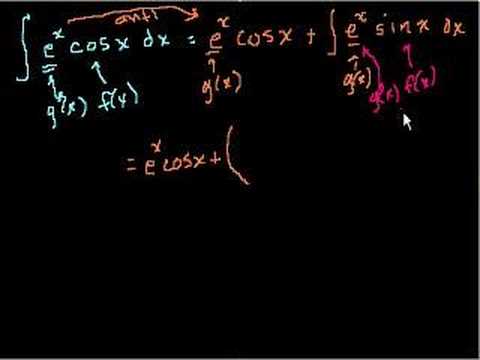
Indefinite Integrals Part 7
-
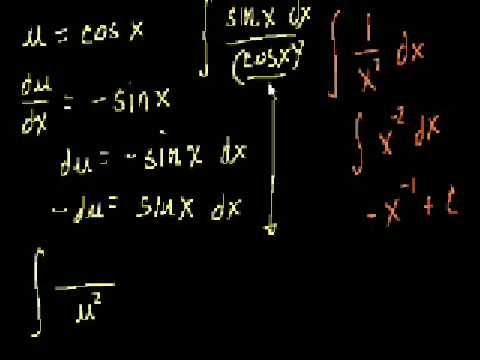
Another U-substitution Example
-

Definite Integrals Part 1
-
Definite Integrals Part 2
-

Definite Integrals Part 3
-
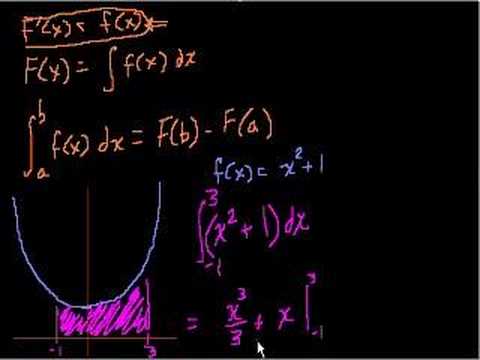
Definite Integrals Part 4
-

Definite Integrals Part 5
-
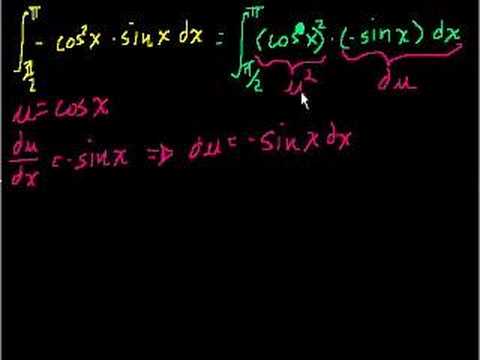
Definite Integral with Substitution
-

Integrals: Trig Substitution Part 1
-

Integrals: Trig Substitution Part 2
-

Integrals: Trig Substitution Part 3
-
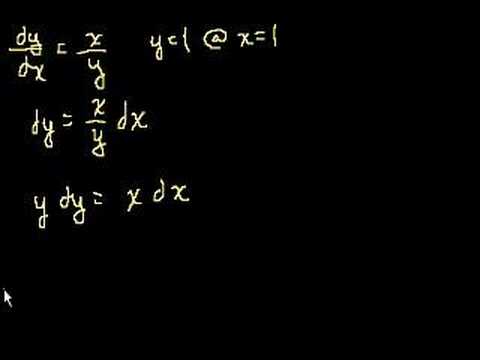
Introduction to Differential Equations
-

Solid of Revolution Part 1
-

Solid of Revolution Part 2
-

Solid of Revolution Part 3
-

Solid of Revolution Part 4
-

Solid of Revolution Part 5
-

Solid of Revolution Part 6
-

Solid of Revolution Part 7
-

Solid of Revolution Part 8
-

Polynomial Approximation of Functions Part 1
-

Polynomial Approximation of Functions Part 2
-

Polynomial Approximation of Functions Part 3
-

Polynomial Approximation of Functions Part 4
-

Polynomial Approximation of Functions Part 5
-

Polynomial Approximation of Functions Part 6
-

Polynomial Approximation of Functions Part 7
-

Taylor Polynomials
-

AP Calculus BC Exams: 2008 1 A
-

AP Calculus BC Exams: 2008 1 B & C
-

AP Calculus BC Exams: 2008 1 C & D
-

AP Calculus BC Exams: 2008 1 D
-

Calculus BC 2008 2 A
-

Calculus BC 2008 2 B & C
-

Calculus BC 2008 2 D
-

Partial Derivatives Part 1
-

Partial Derivatives Part 2
-

Gradient
-

Gradient of a Scalar Field
-

Divergence Part 1
-

Divergence Part 2
-

Divergence Part 3
-

Curl Part 1
-

Curl Part 2
-

Curl Part 3
-

Double Integrals Part 1
-

Double Integrals Part 2
-

Double Integrals Part 3
-

Double Integrals Part 4
-

Double Integrals Part 5
-

Double Integrals Part 6
-

Triple Integrals Part 1
-

Triple Integrals Part 2
-

Triple Integrals Part 3
-

(2^ln x)/x Antiderivative Example
-

Line Integrals
-

Line Integral Example 1
-

Line Integral Example 2 Part 1
-

Line Integral Example 2 Part 2
-

Position Vector Valued Functions
-

Derivative of a Position Vector Valued Function
-

Differential of a Vector Valued Function
-

Differential of a Vector Valued Function Example
-

Line Integrals and Vector Fields
-

Using a Line Integral to Find a Vector Field Example
-

Parametrization of a Reverse Path
-

Scalar Field Line Integral Independent of Path Direction
-

Vector Field Line Integral Dependent of Path Direction
-

Path Independence for Line Integrals
-

Closed Curve Line Integrals of Conservative Vector Fields
-

Example of Closed Line Integral of Conservative Field
-

Second Example of Line Integral of Conservative Vector Field
-

Green's Theorem Proof Part 1
-

Green's Theorem Proof Part 2
-

Green's Theorem Example Part 1
-

Green's Theorem Example Part 2
-

Introduction to Parametrizing a Surface with Two Parameters
-

Position Vector-Valued Function for a Parametrization of Two Parameters
-

Partial Derivatives of Vector-Valued Functions
-

Introduction to the Surface Integral
-

Calculating a Surface Integral Example Part 1
-

Calculating a Surface Integral Example Part 2
-

Calculating a Surface Integral Example Part 3
-

L'Hopital's Rule
-

L'Hopital's Rule Example 1
-

L'Hopital's Rule Example 2
-

L'Hopital's Rule Example 3
-
-
Calculus / First Semester - Limits, Continuity, Derivatives
-

A way to remember the Entire Unit Circle for Trigonometry
-

What is a Limit? Basic Idea of Limits
-
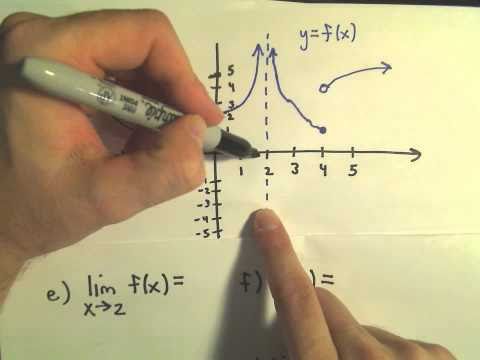
Finding Limits From a Graph
-

Calculating a Limt By Factoring and Canceling
-
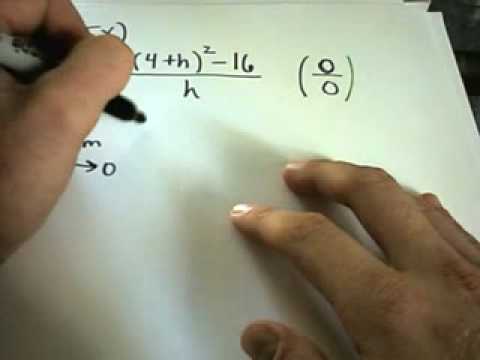
Calculating a Limit by Expanding and Simplfiying
-
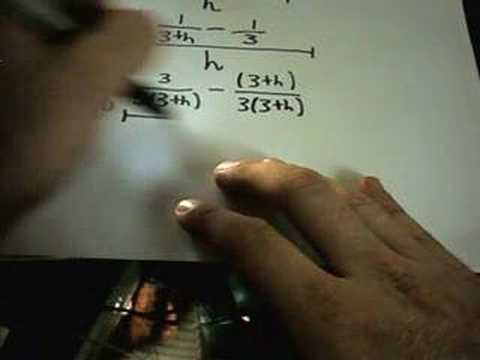
Calculating a Limit by Getting a Common Denominator
-
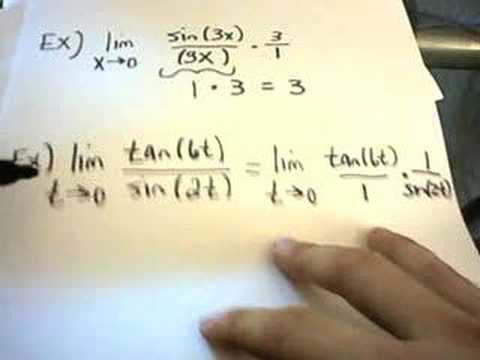
Calculating a Limit Involving sin(x)/x as x approaches zero
-
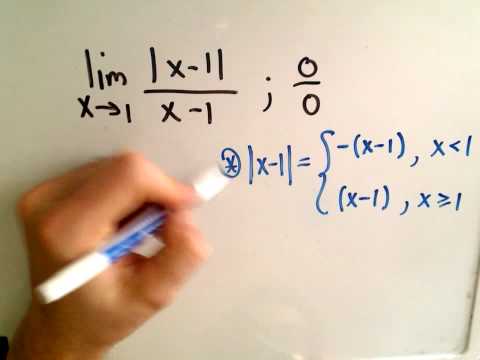
Limits Involving Absolute Value
-
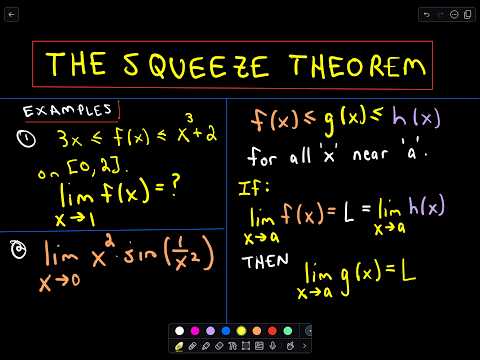
The Squeeze Theorem for Limits, Example 1
-
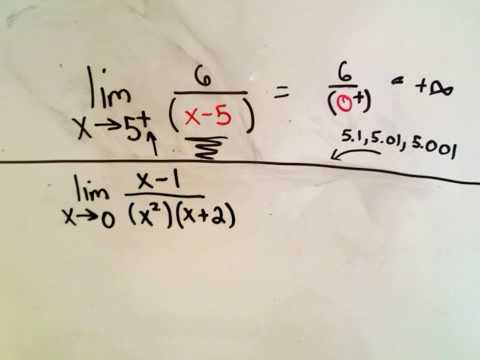
Calculus - Infinite Limits
-

Limits at Infinity - Basic Idea and Shortcuts
-

Shortcut to Find Horizontal Asymptotes of Rational Functions
-

Calculating a Limit at Infinity with a Radical
-
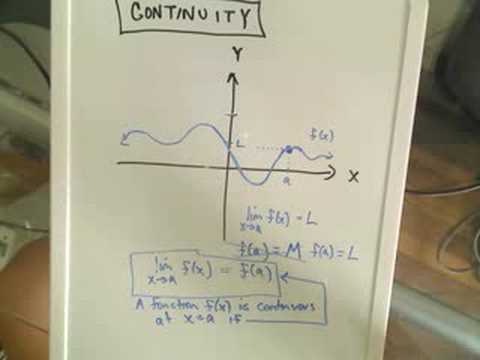
Continuity - Part 1 of 2
-
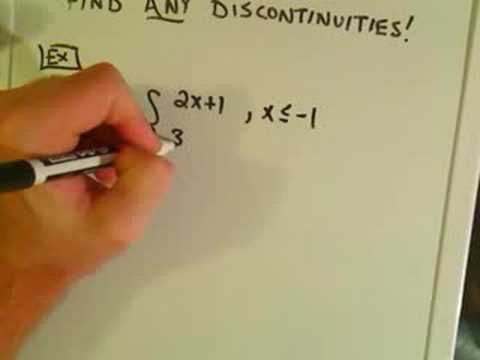
Continuity - Part 2 of 2
-

Understanding the Definition of the Derivative
-
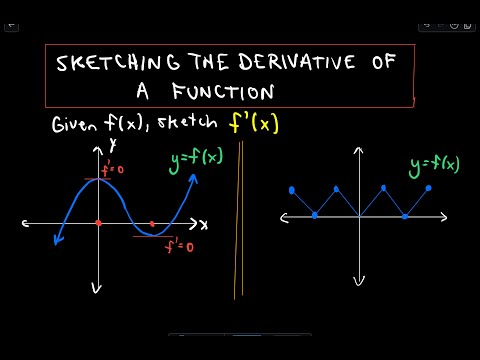
Sketching the Derivative of a Function
-

Finding a Derivative Using the Definition of a Derivative
-

Basic Derivative Examples
-
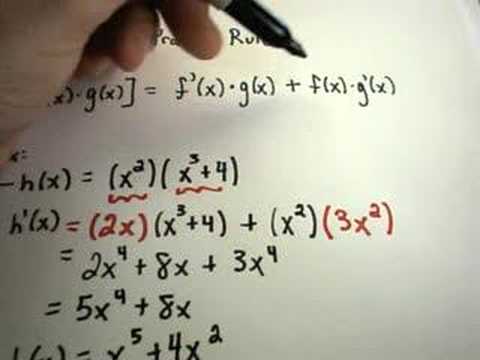
The Product Rule for Derivatives
-

The Quotient Rule
-

Basic Chain Rule Problems
-

Using the Chain Rule - Harder Example #1
-

Using the Chain Rule - Harder Example #2
-
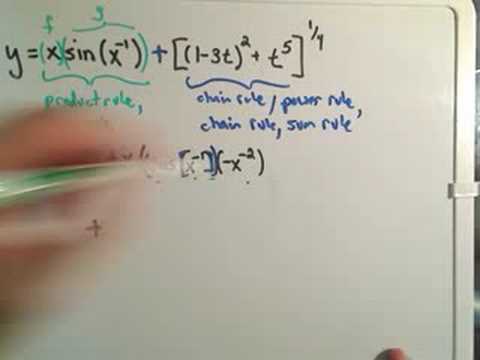
Using the Chain Rule - Harder Example #3
-

Derivatives - Product + Chain Rule + Factoring
-
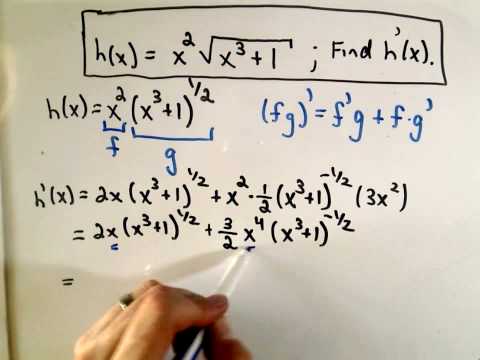
Product Rule, Chain Rule and Factoring - Ex 2
-
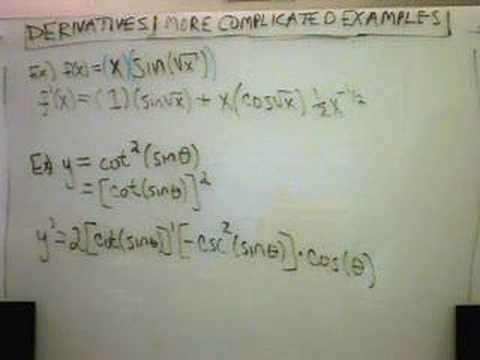
More Complicated Derivative Examples
-
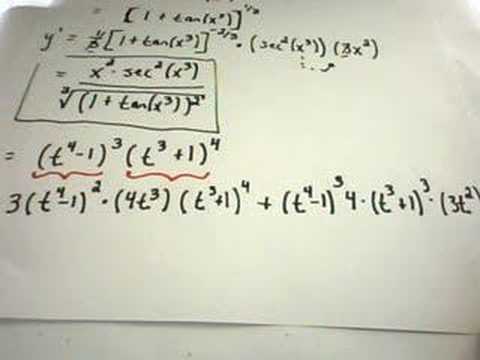
More Complicated Derivative Examples-1
-
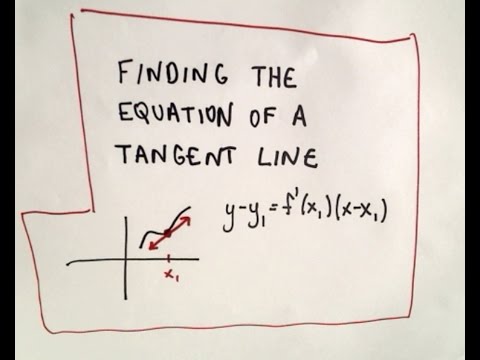
Finding the Equation of a Tangent Line
-

Lots of Different Derivative Examples
-

Implicit Differentiation - Basic Idea and Examples
-
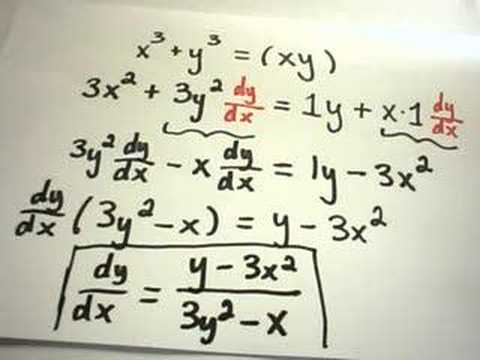
Using Implicit Differentiation - Extra Examples
-
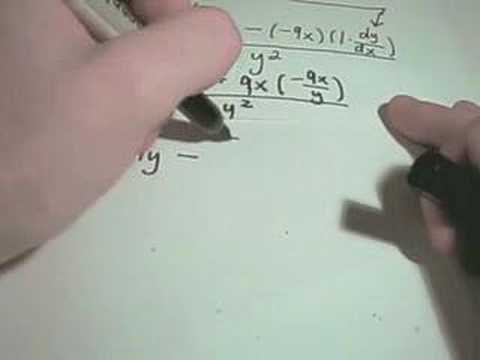
Using Implicit Differentiation - Example
-

Using Implicit Differentiation to find a Second Derivative
-
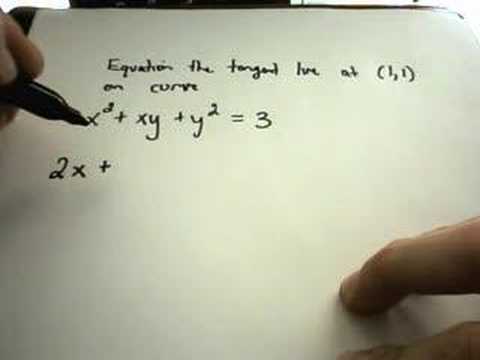
More Implicit Differentiation Examples- 2
-
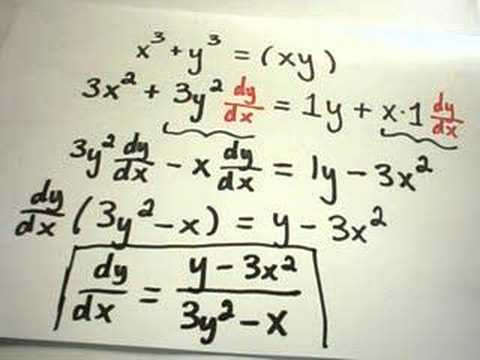
More Implicit Differentiation Examples- 3
-
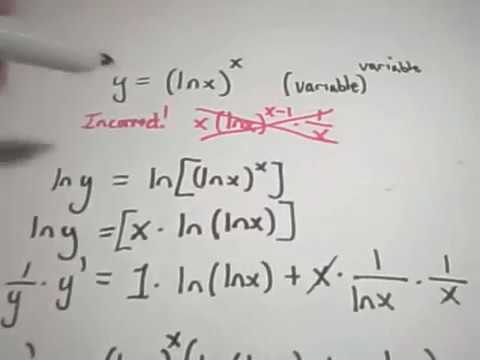
Logarithmic Differentiation
-

Related Rates #1 Problem Using Implicit Differentiation
-

Related Rates #2 Using Cones
-
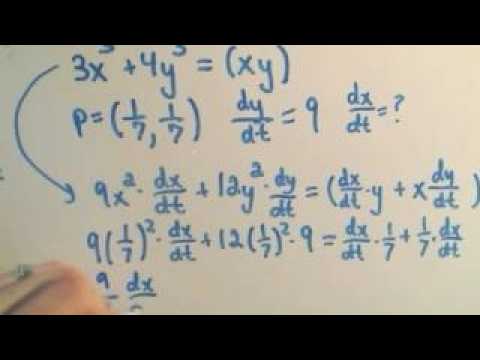
Related Rates #3 - A point on a graph
-

Related Rates #4 Involving Trigonometry
-

Related Rates #5 Involving Baseball
-
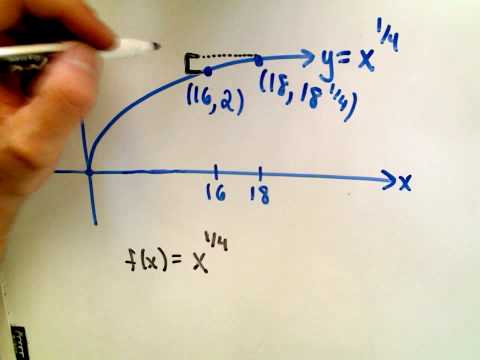
Using Differentials
-
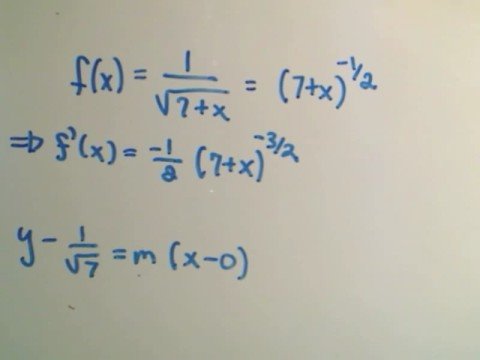
Finding the Linearization at a Point / Tangent Line Approximation
-
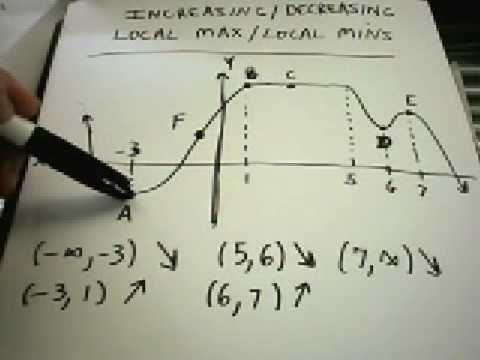
Increasing/Decreasing , Local Maximums/Minimums
-
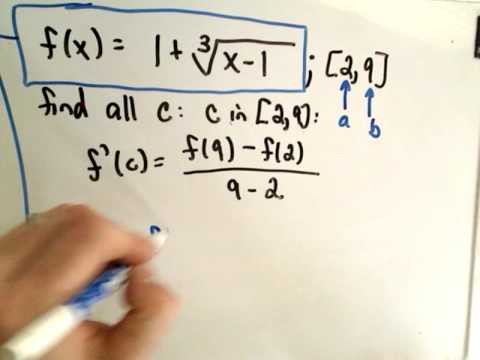
The Mean Value Theorem
-
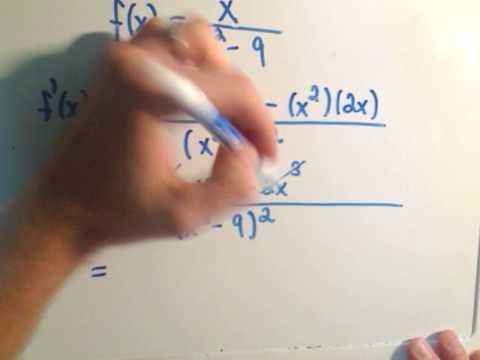
Finding Critical Numbers - Example 1
-

Finding Critical Numbers - Example 2
-

Finding Intervals of Increase/Decrease Local Max/Mins
-
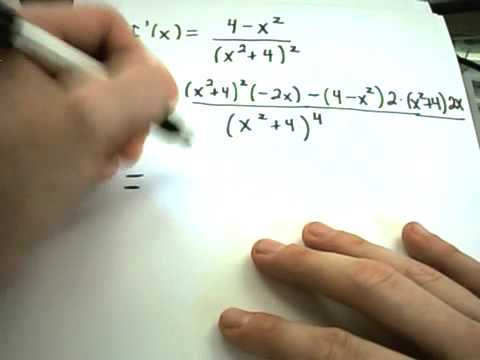
Finding Local Maximums/Minimums - Second Derivative Test
-
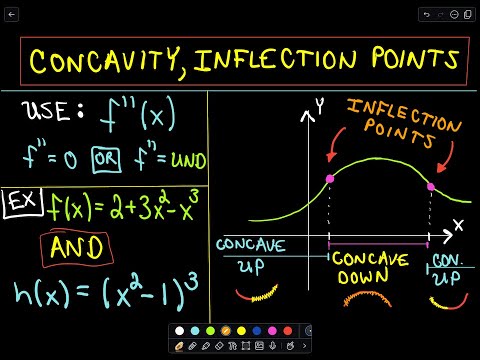
Concavity, Inflection Points and Second Derivatives
-

Curve Sketching Using Calculus - Part 1 of 2
-
Curve Sketching Using Calculus - Part 2 of 2
-

Summary of Curve Sketching - Example 2, Part 1 of 4
-

Summary of Curve Sketching - Example 2 - Part 2 of 4
-

Summary of Curve Sketching - Example 2 - Part 3 of 4
-
Summary of Curve Sketching - Example 2 - Part 4 of 4
-

Optimization Problem #1
-
Optimization Problem #2
-

Optimization Problem #3 - Making a Rain Gutter
-

Newton's Method
-

The Squeeze Theorem and Absolute Value Theorem, #1
-
-
Calculus Revisited: Single Variable Calculus
-

Sets, Functions & Limits- Preface
-

Analytic Geometry
-

Inverse Functions
-

Sets, Functions & Limits- Derivatives and Limits
-

A More Rigorous Approach to Limits
-

Sets, Functions & Limits- Mathematical Inductions
-

Derivatives of Some Simple Functions
-

Approximations and Infinitesimals
-

Composite Functions and the Chain Rule
-

Differentiation of Inverse Functions
-

Implicit Differentiation
-
Differentiation- Continuity
-

Differentiation- Curve Plotting
-

Differentiation- Maxima and Minima
-

Differentiation- Rolle's Theorem and its Consequences
-

Differentiation- Inverse Differentiation
-

Differentiation- The "Definite" Indefinite Integral
-

The Circular Functions
-

Inverse Circular Functions
-

The Definite Integral
-

Marriage of Differential and Integral Calculus
-

Three-Dimensional Area
-

One-Dimensional Area
-

Logarithms without Exponents
-
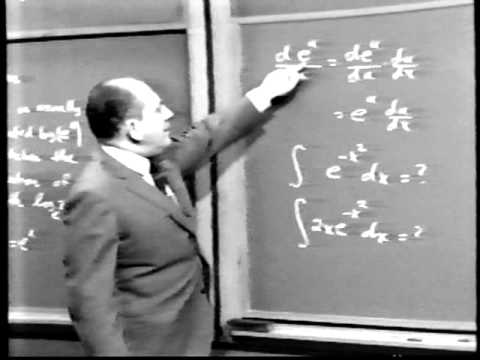
Inverse Logarithms
-

What a Difference a Sign Makes
-

Inverse Hyperbolic Functions
-

More Integration Techniques- Some Basic Recipes
-

More Integration Techniques- Partial Functions
-

More Integration Techniques- Integration by Parts
-

More Integration Techniques- Improper Integrals
-

Infinite Series- Positive Series
-
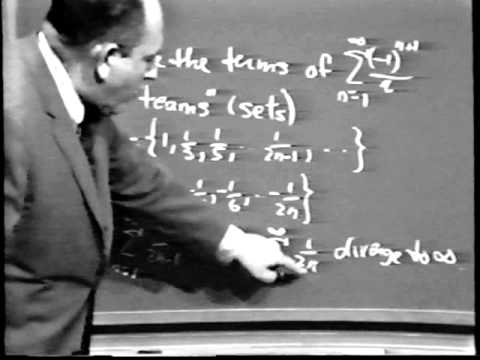
Infinite Series- Absolute Convergence
-

Infinite Series- Polynomial Approximations
-

Infinite Series- Uniform Convergence
-

Infinite Series- Uniform Convergence of Power Series
-
-
Computational Science and Engineering I
-

Positive Definite Matrices K = A'CA
-

One-Dimensional Applications: A = Difference Matrix
-
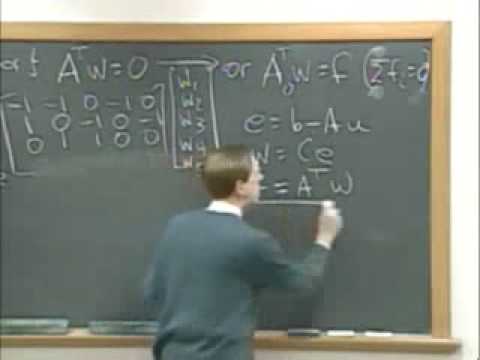
Network Applications: A = Incidence Matrix
-

Applications to Linear Estimation: Least Squares
-

Applications to Dynamics: Eigenvalues of K, Solution of MU'' + KU = F(T)
-

Underlying Theory: Applied Linear Algebra
-

Discrete Vs. Continuous: Differences and Derivatives
-

Applications to Boundary Value Problems: Laplace Equation
-

Solutions of Laplace Equation: Complex Variables
-

Delta Function and Green's Function
-
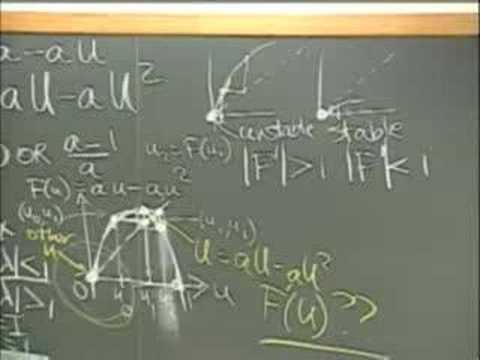
initial Value Problems: Wave Equation and Heat Equation
-

Solutions of initial Value Problems: Eigenfunctions
-

Numerical Linear Algebra: Orthogonalization and A = QR
-

Numerical Linear Algebra: SVD and Applications
-

Numerical Methods in Estimation: Recursive Least Squares and Covariance Matrix
-

Dynamic Estimation: Kalman Filter and Square Root Filter
-

Finite Difference Methods: Equilibrium Problems
-

Finite Difference Methods: Stability and Convergence
-

Optimization and Minimum Principles: Euler Equation
-

Finite Element Method: Equilibrium Equations
-

Spectral Method: Dynamic Equations
-

Fourier Expansions and Convolution
-

Fast Fourier Transform and Circulant Matrices
-

Discrete Filters: Lowpass and Highpass
-

Filters in the Time and Frequency Domain
-
Filter Banks and Perfect Reconstruction
-
Multiresolution, Wavelet Transform and Scaling Function
-

Splines and Orthogonal Wavelets: Daubechies Construction
-
Applications in Signal and Image Processing: Compression
-

Network Flows and Combinatorics: Max Flow = Min Cut
-

Simplex Method in Linear Programming
-
Nonlinear Optimization: Algorithms and Theory
-
-
Convex Optimization I
-

Introduction to Convex Optimization I
-

Guest Lecturer: Jacob Mattingley
-

Logistics
-

Vector Composition
-

Optimal And Locally Optimal Points
-

(Generalized) Linear-Fractional Program
-

Generalized Inequality Constraints
-

Lagrangian
-

Complementary Slackness
-

Applications Section of Course
-

Statistical Estimation
-
Continue On Experiment Design
-

Linear Discrimination (Cont.)
-

LU Factorization (Cont.)
-

Algorithm Section of The Course
-

Continue on Unconstrained Minimization
-

Newton's Method (Cont.)
-

Logarithmic Barrier
-

Interior-Point Methods (Cont.)
-
-
Convex Optimization II
-

Basic Rules for Subgradient Calculus
-

Recap: Subgradients
-

Convergence Proof, Stopping Criterion
-

Project Subgradient For Dual Problem
-

Stochastic Programming
-

Addendum: Hit-And-Run CG Algorithm
-

Example: Piecewise Linear Minimization
-

Recap: Ellipsoid Method
-

Comments: Latex Typesetting Style
-

Decomposition Applications
-
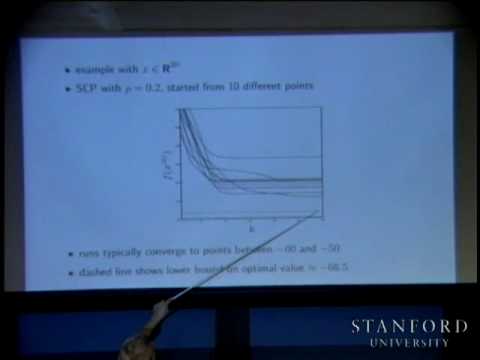
Sequential Convex Programming
-

Recap: 'Difference Of Convex' Programming
-

Recap: Conjugate Gradient Method
-

Methods (Truncated Newton Method)
-

Recap: Example: Minimum Cardinality Problem
-

Model Predictive Control
-

Stochastic Model Predictive Control
-

Recap: Branch And Bound Methods, Basic Idea, Unconstrained, Nonconvex Minimization
-
-
Developmental Math
-

Place Value 1
-

Place Value 2
-

Place Value 3
-

Rounding Whole Numbers 1
-

Rounding Whole Numbers 2
-

Rounding Whole Numbers 3
-

Comparing Whole Numbers 1
-

Comparing Whole Numbers 2
-

Comparing Whole Numbers 3
-

Adding Whole Numbers and Applications 1
-
Adding Whole Numbers and Applications 2
-
Adding Whole Numbers and Applications 3
-
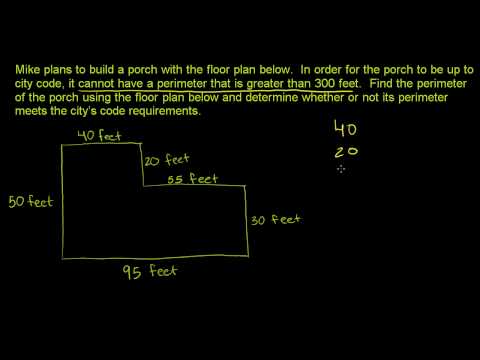
Adding Whole Numbers and Applications 4
-
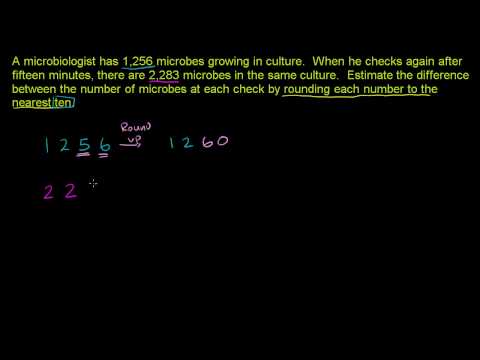
Rounding to Estimate Difference
-

Rounding to Estimate Sums 1
-

Rounding to Estimate Sums 2
-

Multiplying Whole Numbers and Applications 1
-

Multiplying Whole Numbers and Applications 2
-

Multiplying Whole Numbers and Applications 3
-

Multiplying Whole Numbers and Applications 4
-
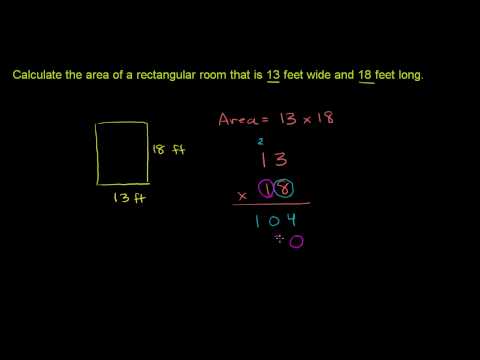
Multiplying Whole Numbers and Applications 5
-

Area of a Circle
-